VINS-Mono 中的 Marginalization

发表于 | 分类于 ， | | 阅读次数:
VINS-Mono中的 Marginalization 相关代码学习

摘要

几乎所有基于优化的VIO系统，都会提到利用 Marginalization 的方式，保留与滑窗滑出去的状态量相关的约束。让我们来看看在 VINS-Mono 的代码中，对于 Marginalization 是怎么操作的。

Marginalization 基础

简单回顾一下 Marginalization 的基本原理。这部分内容参考了贺博、Lemonade_和 Hansry 的博客。[1][2][3]

在 GN 或者 LM 求解非线性优化问题的时候，本质上就是求解: $ H \delta x = b $
其中 $ H = J^T J, b = J^Te$，$J$ 表示对应状态量下的雅可比矩阵，$e$ 表示对应状态量下的残差项。

可以人为地将 $\delta x$ 分为 $\delta x_1$ 和 $\delta x_2$两部分，因此有
$$ \begin{bmatrix}
H_{11} & H_{12} \\
H_{21} & H_{22}
\end{bmatrix} \begin{bmatrix}
\delta x_1 \\
\delta x_2
\end{bmatrix} = \begin{bmatrix}
b_1 \\
b_2
\end{bmatrix} $$

假设要丢弃 $x_2$，通过高斯消元的方式，可以得到 $ (H_{11} - H_{12}H_{22}^{-1}H_{21})\delta x_1 = b_1 - H_{12}H_{22}^{-1}b_2 $
通过这种方式，即使不求解 $x_2$，也可以得到 $x_1$的解。这个过程在数学上被成为舒尔补。

对应到SLAM问题中，如下图中表示的因子图，我们想要边缘化滑窗内最前面的关键帧 $X_{p1}$。则 $X_{p1}$ 即为上述式子中的 $x_2$，其他关键帧和地图点为 $x_1$

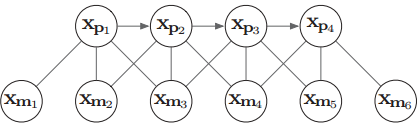
因此我们利用舒尔补可以将上图变换为下图。

神奇的事情就这么发生了，$X_{p1}$就这样消失了，但是对于剩余状态量的求解没有发生任何信息上的损失。
其对应的信息矩阵$H = (H_{11} - H_{12}H_{22}^{-1}H_{21}) = J^TJ$
其对应的$b = b_1 - H_{12}H_{22}^{-1}b_2 = J^Te$，则对应的残差为 $e = (J^T)^{-1} b$

这部分即可认为是边缘化$X_{p1}$时，对剩余状态量留下的残差项以及对应的雅可比矩阵。即使后续滑窗中补入了新的关键帧以及地图点，这部分残差依旧会在非线性优化过程中被考虑。

不过还遗留一个非常关键的问题，由于剩余状态量还在滑窗内会被继续优化，当引入新的观测后，这些状态量是会发生变化的，此时就和边缘化$X_{p1}$时的状态量不一样了，从而导致雅可比和残差项都发生了变化。
这下完犊子了，$X_{p1}$已经被丢掉了，已经不可能再把$X_{p1}$拿回来重新再计算了。因此，这里就第一次引入了 First Estimate Jocabian(FEJ)的概念。既然没法重新算雅可比，那干脆直接就固定雅可比，然后用这个固定的雅可比利用一阶泰勒展开去估计新的残差$e^{*}$。即 $e^{*} = e + J dx$

至此有了关于边缘化的雅可比和会不断更新的残差，边缘化的信息就会在后续的非线性优化过程中被保留。

VINS-Mono中 的 Marginalization

弄明白了 Marginalization 的理论基础，再来看 VINS-Mono 中的相关代码，就非常的丝般顺滑了。我们先看要边缘化滑窗中最前面一个关键帧，VINS-Mono是怎么实现的。

先明确几个关键的变量，直接看注释。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
vector<double *> last_marginalization_parameter_blocks; //本次边缘化需要保留的状态量的内存地址
struct ResidualBlockInfo
{
    std::vector<double *> parameter_blocks; //优化变量内存地址
    std::vector<int> drop_set; //需要被边缘化的变量地址的id，也就是上面这个vector的id
    double **raw_jacobians;
    Eigen::VectorXd residuals;
};
class MarginalizationInfo
{
    std::vector<ResidualBlockInfo *> factors; //保存了视觉观测项，imu观测项以及上一次的边缘化项，从中去分离出需要边缘化的状态量和需要保留的状态量
    int m, n; //m为要边缘化的变量个数，n为要保留下来的变量个数
    std::unordered_map<long, int> parameter_block_size; //<优化变量内存地址, localSize>
    int sum_block_size;
    std::unordered_map<long, int> parameter_block_idx; //<优化变量内存地址, 在矩阵中的id>
    std::unordered_map<long, double *> parameter_block_data;//<优化变量内存地址, 数据>
    std::vector<int> keep_block_size; //按顺序存放上面的 parameter_block_size 中被保留的优化变量
    std::vector<int> keep_block_idx;  //按顺序存放上面的 parameter_block_idx 中被保留的优化变量
    std::vector<double *> keep_block_data; //按顺序存放上面的 parameter_block_data 中被保留的优化变量
    Eigen::MatrixXd linearized_jacobians; //边缘化得到的雅可比矩阵
    Eigen::VectorXd linearized_residuals; //边缘化得到的残差
};

首先，是要把所有观测，包括视觉观测项，IMU观测项以及上一次的边缘化信息都添加进来。通过这些信息可以计算当前状态量下的雅可比和残差。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
//添加上一次的边缘化信息
vector<int> drop_set;
for (int i = 0; i < static_cast<int>(last_marginalization_parameter_blocks.size()); i++)
{
    if (last_marginalization_parameter_blocks[i] == para_Pose[0] ||
        last_marginalization_parameter_blocks[i] == para_SpeedBias[0])
        drop_set.push_back(i);)//需要边缘化掉滑窗内第一个帧的优化变量
}
// construct new marginlization_factor
MarginalizationFactor *marginalization_factor = new MarginalizationFactor(last_marginalization_info);
ResidualBlockInfo *residual_block_info = new ResidualBlockInfo(marginalization_factor, NULL,
                                                                last_marginalization_parameter_blocks,
                                                                drop_set);
marginalization_info->addResidualBlockInfo(residual_block_info); 
//添加滑窗内第一帧和第二帧之间的IMU观测项
IMUFactor* imu_factor = new IMUFactor(pre_integrations[1]);
ResidualBlockInfo *residual_block_info = new ResidualBlockInfo(imu_factor, NULL,
                                                        vector<double *>{para_Pose[0], para_SpeedBias[0], para_Pose[1], para_SpeedBias[1]},
                                                        vector<int>{0, 1}); //需要边缘化掉 para_Pose[0], para_SpeedBias[0]
marginalization_info->addResidualBlockInfo(residual_block_info);  
//添加地图点第一次观测发生在滑窗内第一帧的视觉观测项
int imu_i = it_per_id.start_frame, imu_j = imu_i - 1;
if (imu_i != 0)
    continue;
Vector3d pts_i = it_per_id.feature_per_frame[0].point;
for (auto &it_per_frame : it_per_id.feature_per_frame)
{
    imu_j++;
    if(imu_i != imu_j)
    {
        Vector3d pts_j = it_per_frame.point;
        ProjectionTwoFrameOneCamFactor *f_td = new ProjectionTwoFrameOneCamFactor(pts_i, pts_j, it_per_id.feature_per_frame[0].velocity, it_per_frame.velocity,
                                                            it_per_id.feature_per_frame[0].cur_td, it_per_frame.cur_td);
        ResidualBlockInfo *residual_block_info = new ResidualBlockInfo(f_td, loss_function,
                                                                        vector<double *>{para_Pose[imu_i], para_Pose[imu_j], para_Ex_Pose[0], para_Feature[feature_index], para_Td[0]},
                                                                        vector<int>{0, 3}); //需要边缘化掉 para_Pose[0]和对应的地图点，这里的imu_i永远等于0
        marginalization_info->addResidualBlockInfo(residual_block_info);
    }
}

之后是调用 preMarginalize 函数得到各个观测的雅可比和残差，顺带把优化变量的值给拷贝出来

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void MarginalizationInfo::preMarginalize()
{
    for (auto it : factors)
    {
        it->Evaluate();  //get parameter block addr(parameter_blocks), residual, jacobian 
        std::vector<int> block_sizes = it->cost_function->parameter_block_sizes();
        for (int i = 0; i < static_cast<int>(block_sizes.size()); i++)
        {
            long addr = reinterpret_cast<long>(it->parameter_blocks[i]);
            int size = block_sizes[i];
            if (parameter_block_data.find(addr) == parameter_block_data.end())
            {
                double *data = new double[size];
                memcpy(data, it->parameter_blocks[i], sizeof(double) * size);
                parameter_block_data[addr] = data; //get parameter data, rather than addr any more
            }
        }
    }
}

最后是通过调用 marginalize 函数得到本次边缘化的结果，即边缘化的雅可比矩阵和残差

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
void MarginalizationInfo::marginalize()
{
    int pos = 0;
    for (auto &it : parameter_block_idx)
    {
        it.second = pos;
        pos += localSize(parameter_block_size[it.first]);
    } //得到每个被边缘化的优化变量在矩阵中的位置
    m = pos;
    for (const auto &it : parameter_block_size)
    {
        if (parameter_block_idx.find(it.first) == parameter_block_idx.end())
        {
            parameter_block_idx[it.first] = pos;
            pos += localSize(it.second);
        }
    }//得到每个被保留的优化变量在矩阵中的位置
    n = pos - m;
    Eigen::MatrixXd A(pos, pos); //把要被边缘化的优化变量对应的H矩阵放到左上角
    Eigen::VectorXd b(pos); //把要被边缘化的优化变量对应的b放到左边
    for (auto it : factors)
    {
        for (int i = 0; i < static_cast<int>(it->parameter_blocks.size()); i++)
        {
            int idx_i = parameter_block_idx[reinterpret_cast<long>(it->parameter_blocks[i])];
            int size_i = localSize(parameter_block_size[reinterpret_cast<long>(it->parameter_blocks[i])]);
            Eigen::MatrixXd jacobian_i = it->jacobians[i].leftCols(size_i);
            for (int j = i; j < static_cast<int>(it->parameter_blocks.size()); j++)
            {
                int idx_j = parameter_block_idx[reinterpret_cast<long>(it->parameter_blocks[j])];
                int size_j = localSize(parameter_block_size[reinterpret_cast<long>(it->parameter_blocks[j])]);
                Eigen::MatrixXd jacobian_j = it->jacobians[j].leftCols(size_j);
                if (i == j)
                    A.block(idx_i, idx_j, size_i, size_j) += jacobian_i.transpose() * jacobian_j;
                else
                {
                    A.block(idx_i, idx_j, size_i, size_j) += jacobian_i.transpose() * jacobian_j;
                    A.block(idx_j, idx_i, size_j, size_i) = A.block(idx_i, idx_j, size_i, size_j).transpose();
                }
            }
            b.segment(idx_i, size_i) += jacobian_i.transpose() * it->residuals;
        }
    }
    Eigen::MatrixXd Amm = 0.5 * (A.block(0, 0, m, m) + A.block(0, 0, m, m).transpose()); //A的左上角矩阵，保证Amm是对称矩阵
    Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes(Amm);
    Eigen::MatrixXd Amm_inv = saes.eigenvectors() * Eigen::VectorXd((saes.eigenvalues().array() > eps).select(saes.eigenvalues().array().inverse(), 0)).asDiagonal() * saes.eigenvectors().transpose();
    
    Eigen::VectorXd bmm = b.segment(0, m);
    Eigen::MatrixXd Amr = A.block(0, m, m, n);
    Eigen::MatrixXd Arm = A.block(m, 0, n, m);
    Eigen::MatrixXd Arr = A.block(m, m, n, n);
    Eigen::VectorXd brr = b.segment(m, n);
    A = Arr - Arm * Amm_inv * Amr;
    b = brr - Arm * Amm_inv * bmm; //对应舒尔补公式
    Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes2(A);
    Eigen::VectorXd S = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array(), 0));
    Eigen::VectorXd S_inv = Eigen::VectorXd((saes2.eigenvalues().array() > eps).select(saes2.eigenvalues().array().inverse(), 0));
    Eigen::VectorXd S_sqrt = S.cwiseSqrt();
    Eigen::VectorXd S_inv_sqrt = S_inv.cwiseSqrt();
    //对A进行特征值分解 A = eigenvectors * eigenvalues.asDiagonal() * eigenvectors.transpose() = JTJ
    //J = sqrt(eigenvalues.asDiagonal()) * eigenvectors.transpose()
    linearized_jacobians = S_sqrt.asDiagonal() * saes2.eigenvectors().transpose();
    linearized_residuals = S_inv_sqrt.asDiagonal() * saes2.eigenvectors().transpose() * b;

最后来看看怎么利用边缘化得到的雅可比和残差，构造先验信息进入到非线性优化的。即对应的 MarginalizationFactor::Evaluate 函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
bool MarginalizationFactor::Evaluate(double const *const *parameters, double *residuals, double **jacobians) const
{
    int n = marginalization_info->n; // 保留的状态变量数目
    int m = marginalization_info->m; // 被边缘化的状态变量数目
    Eigen::VectorXd dx(n); //dx表示当前的状态量和边缘化时的状态量之间的差值
    for (int i = 0; i < static_cast<int>(marginalization_info->keep_block_size.size()); i++)
    {
        int size = marginalization_info->keep_block_size[i]; //dimension of every sensor, accumulate keep_block_size equals m
        int idx = marginalization_info->keep_block_idx[i] - m;
        Eigen::VectorXd x = Eigen::Map<const Eigen::VectorXd>(parameters[i], size); //当前优化过程中，被保留的状态量的值
        Eigen::VectorXd x0 = Eigen::Map<const Eigen::VectorXd>(marginalization_info->keep_block_data[i], size); //边缘化时，被保留的状态量的值 
        if (size != 7)
            dx.segment(idx, size) = x - x0;
        else
        {
            dx.segment<3>(idx + 0) = x.head<3>() - x0.head<3>();
            dx.segment<3>(idx + 3) = 2.0 * Utility::positify(Eigen::Quaterniond(x0(6), x0(3), x0(4), x0(5)).inverse() * Eigen::Quaterniond(x(6), x(3), x(4), x(5))).vec();
            if (!((Eigen::Quaterniond(x0(6), x0(3), x0(4), x0(5)).inverse() * Eigen::Quaterniond(x(6), x(3), x(4), x(5))).w() >= 0))
            {
                dx.segment<3>(idx + 3) = 2.0 * -Utility::positify(Eigen::Quaterniond(x0(6), x0(3), x0(4), x0(5)).inverse() * Eigen::Quaterniond(x(6), x(3), x(4), x(5))).vec();
            }
        }//两个状态量的差
    }
    Eigen::Map<Eigen::VectorXd>(residuals, n) = marginalization_info->linearized_residuals + marginalization_info->linearized_jacobians * dx; //和上一章节推导的一样
    if (jacobians)
    {
        for (int i = 0; i < static_cast<int>(marginalization_info->keep_block_size.size()); i++)
        {
            if (jacobians[i])
            {
                int size = marginalization_info->keep_block_size[i], local_size = marginalization_info->localSize(size);
                int idx = marginalization_info->keep_block_idx[i] - m;
                Eigen::Map<Eigen::Matrix<double, Eigen::Dynamic, Eigen::Dynamic, Eigen::RowMajor>> jacobian(jacobians[i], n, size);
                jacobian.setZero();
                jacobian.leftCols(local_size) = marginalization_info->linearized_jacobians.middleCols(idx, local_size);
            }
        } //拿到对应的雅可比
    }
    return true;
}

最后的最后，不要忘记，由于滑窗是会改变优化变量的地址的，因此对被保留的优化变量的地址进行更新。

1
2
3
4
5
6
7
8
9
10
11
12
13
std::unordered_map<long, double *> addr_shift;
for (int i = 1; i <= WINDOW_SIZE; i++)
{
    addr_shift[reinterpret_cast<long>(para_Pose[i])] = para_Pose[i - 1];
    if(USE_IMU)
        addr_shift[reinterpret_cast<long>(para_SpeedBias[i])] = para_SpeedBias[i - 1];
}
for (int i = 0; i < NUM_OF_CAM; i++)
    addr_shift[reinterpret_cast<long>(para_Ex_Pose[i])] = para_Ex_Pose[i];
addr_shift[reinterpret_cast<long>(para_Td[0])] = para_Td[0];
vector<double *> parameter_blocks = marginalization_info->getParameterBlocks(addr_shift);

至此，VINS-Mono的边缘化滑窗中最前面的关键帧的流程就走完了。
而边缘化滑窗中最新的非关键帧，就不再展开叙述了，基本上是大同小异的。

再谈 FEJ

之前在Marginalization 基础章节中提到，由于我们已经把边缘化的优化变量丢弃了，因此当被保留的优化变量发生变化时，是无法对雅可比进行更新。因此针对这种情况，固定雅可比更像是一种无奈之举。

而其实不仅仅针对边缘化的雅可比，其实针对整个优化问题来说，也会存在求解雅可比时，线性展开的位置不一致。
再来看下图。假设这个时候我们引入了新的视觉观测 $X_{m7}$，而且 $X_{m7}$ 与 $X_{p4}$ 产生了约束。因此对于 $X_{p4}$，边缘化的残差对于$X_{p4}$的雅可比从边缘化发生时就已经固定不变了，而 $X_{m7}$ 对于 $X_{p4}$ 的雅可比却可以随着优化的迭代过程中不断被更新，这就导致了对于 $X_{p4}$ 来说，在同一个优化问题里，在两个不同的位置被线性展开，这可能会导致其信息矩阵的零空间发生变化，从而在求解时引入错误信息。因此，为了保证一致性，对于有边缘化信息的非线性优化问题，所有的优化变量的雅可比都应该使用优化迭代开始前的雅可比，在优化迭代的过程中不发生变化。这就是真正意义上的 FEJ！

然而….，VINS-Mono并没有这么做，因为据作者说，在VINS-Mono中使用FEJ的实际效果不如不使用FEJ…

卒…

参考文献

[1] SLAM中的marginalization 和 Schur complement
[2] VINS-MONO边缘化策略
[3] VSLAM之边缘化 Marginalization 和 FEJ (First Estimated Jocobian)
[4] VINS-Mono关键知识点总结——边缘化marginalization理论和代码详解
[5] VINS-Mono: A Robust and Versatile Monocular Visual-Inertial State Estimator
[6] Decoupled, consistent node removal and edge sparsification for graph-based SLAM
[7] Sliding window filter with application to planetary landing