摘要

一个 Visual Odometry 即使做的再牛逼，累积误差依旧是无法避免的。而 GPS 是一种全局观测的传感器，每一次观测都是独立的，因此误差并不会累积。从理论上看，将一个局部精度很高但存在累积误差的 Visual Odometry 和一个局部精度无法保证到不存在累积误差的 GPS 相结合，可以得到一个很美秒的结果。在调研了相关的 paper 之后，GPS 和 Visual Odometry 相结合的方法依旧可以分为滤波和优化两种方式。

滤波

A Robust and Modular Multi-Sensor Fusion Approach Applied to MAV Navigation (IROS 2013, ETH)
ETH 2013年出的融合多传感器的松耦合滤波方法，代码开源，并且已经集成到 ROS 里面。
其主要思想是把 IMU 作为主传感器，通过积分得到6自由度的pose。VO（VIO）作为相对位姿的估计器，GPS 等作为全局位姿估计器，与 IMU 积分得到的结果进行 EKF，得到更加准确的位置估计。IMU 积分受到 bias 和噪声的印象，会很快的发散。而VO可以认为在局部范围内误差很小，因此可以修正 IMU 的 bias。而 GPS 不存在累积误差的问题，又可以修正 IMU 和 VO（VIO）的累积误差。
作为主传感器，IMU 需要估计的状态量如下图所示。包括旋转，速度，平移，陀螺仪的 bias 和加速度计的 bias。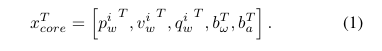

而当要融合单目VO时，由于单目VO无法估计尺度，并且存在一定的累积误差，因此在状态量中添加了尺度估计，平移漂移估计，旋转漂移估计以及 IMU-Camera 的旋转外参。作者认为 IMU-Camera的平移外参不怎么会变，因此忽略了这一项。
添加的状态量如下图所示。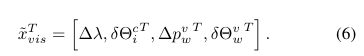

此时可以得到观测模型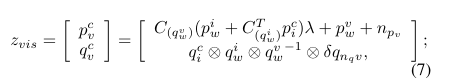

线性化以后得到的观测方程为：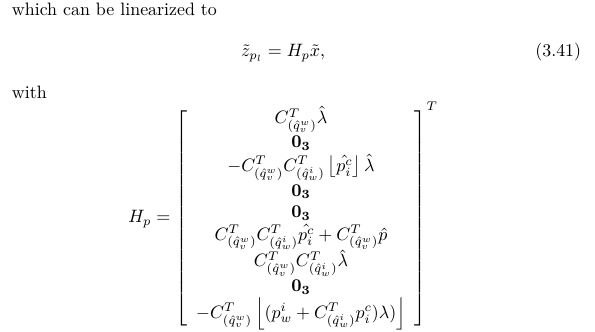

至此就可以通过EKF的方式进行IMU传感器和单目VO的融合。
同样的，GPS 的观测方程比较简单，即将待估计的 pose 通过外参转化到 GPS 坐标系的 pose，因为 GPS 无法测量旋转，所以直接取三维位置的差作为观测误差。

由于 VO 的尺度漂移是不稳定的，因此直接把 VO 的pose放在全局坐标系下建立观测方程去估计尺度是不够准确的，因此作者提出了把 VO 的 pose 作为两帧之间相对的 delta pose 去建立观测方程。
大致的思路就是把带估计的状态量的 pose 由1个变为2个，然后基于这个去建立协防差估计和观测方程。如下图所示。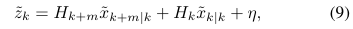

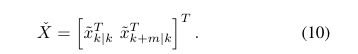
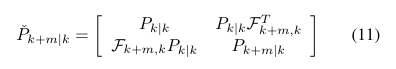
论文中还提到了一些细节，比如处理了诸如时延造成的更新方程会落后于预测方程的情况，异常检测等。有兴趣的可以详见paper。

优化

A General Optimization-based Framework for Global Pose Estimation with Multiple Sensors (HKUST)
这篇文章是港科大沈老师组基于 vins-mono 进行的拓展。支持双目配置、多轨迹融合以及GPS等全局传感器与VO进行联合优化。我们着重看一下 GPS 部分是如何与 VO 进行联合优化的。
对于视觉、IMU等传感器，由于其无法获得全局信息，因此被定义为 local sensors。而对于GPS、磁力计等能够感知全局信息的传感器，被定义为 global sensors。
对于 local sensors，首先进行局部位姿估计，即传统意义上的 VO 或者 VIO。得到局部的位姿估计之后，再与 GPS 等全局传感器进行对齐。对齐的方式是建立一个 posegraph，每个 GPS 时刻建立一个位姿 node，连续的两个 node 之间将局部位姿估计得到的 delta pose 作为约束。每个 node 还与 GPS 等全局位置建立约束。如下图所示。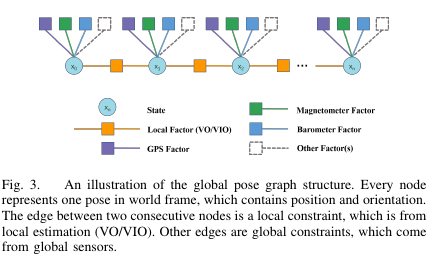

GOMSF: Graph-Optimization based Multi-Sensor Fusion for robust UAV pose estimation（ICRA 2018，ETH）
这篇文章出自ETH，总体思想上与上一篇大差不差，但细节上和实验上更加完备一些。如下图所示。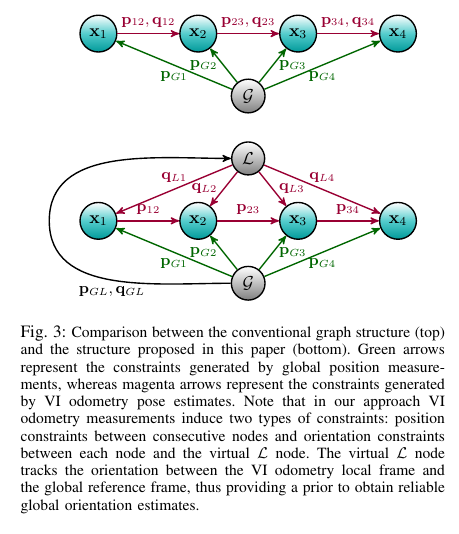

上半部分的 pose graph 结构即为第一篇文章的结构。但是作者认为，GPS 无法提供旋转的约束，因此基于这种结构优化后的旋转的精度会变差。因此提出了第二种 pose graph 结构。
其中 GPS 部分的约束保持不变。但 delta pose 只利用 VO(VIO) 的平移部分建立 node 和 node 之间的约束。而旋转则通过建立一个虚拟的局部坐标系，通过计算局部坐标系和全局坐标系（GPS坐标系）之间的变换 $_GT_L$，建局部坐标系下的旋转转换成全局坐标系下的旋转，然后建立全局的旋转约束。在初始化阶段，通过直接对齐 VO(VIO) pose 和 GPS，解SVD来求解$_GT_L$。而后续优化过程中，首先固定$_GT_L$，滑窗优化完成后，通过对齐 VO(VIO) pose和优化后的pose得到新的 $_GT_L$。理论上讲，当 VO(VIO) 的局部误差够小，一定范围内 $_GT_L$ 是基本保持不变的。因此每个 VO(VIO) 时刻的局部 pose，都可以通过 $_GT_L$ 变成全局 pose。

这篇文章的实验部分特意证明了自己的方法要由于滤波方法和第一篇文章的方法。对比实验如下：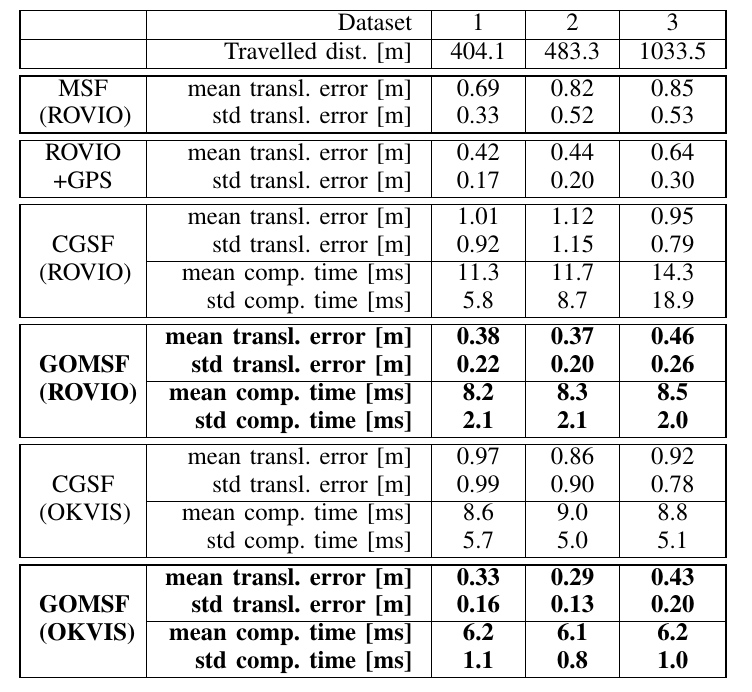

而通过全局约束的方法，也提升了旋转的精度。如下图所示。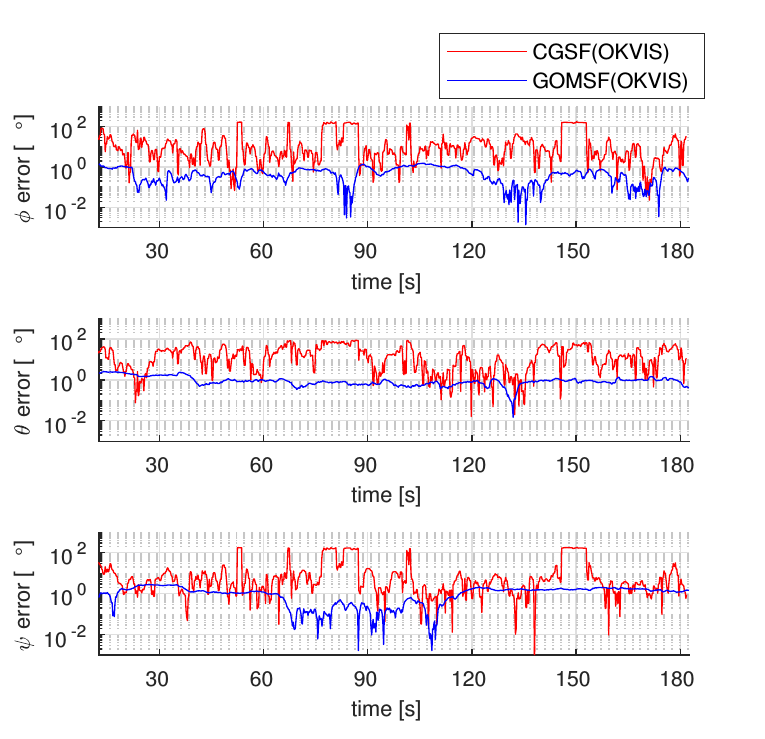

还有一个细节就是，在进行优化之前，作者会把 VO(VIO) 出的 pose 与 IMU 进行一次松耦合的滤波。尽量减少与 GPS 之间的时延带来的误差。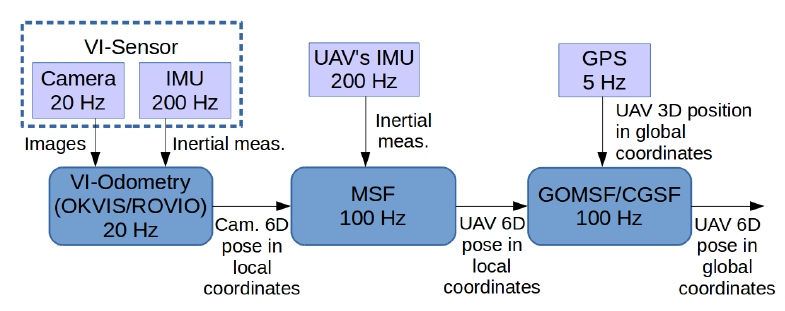

小结

总体来说，融合 GPS 的方法并没有什么特别令人经验的地方，里面也有很多细节值得思考。最直接的问题就是如何估计一个比较好的方差，无论是视觉方差还是 GPS 方差。比如 GPS 方差，如果 GPS 的位置比较扯淡，但自己又认为自己的方差很小，那么很有可能把整体的 pose 拉歪。VINS-Fusion直接采用了 GPS 的星数作为方差估计的标准，即星数越多方差越小。
实际应用过程中应该还有很多坑要采。待实操后在更新。

文献

[1] Lynen S, Achtelik M W, Weiss S, et al. A robust and modular multi-sensor fusion approach applied to mav navigation[C]//2013 IEEE/RSJ international conference on intelligent robots and systems. IEEE, 2013: 3923-3929.
[2] Weiss S M. Vision based navigation for micro helicopters[D]. ETH Zurich, 2012.
[3] Qin T, Cao S, Pan J, et al. A General Optimization-based Framework for Global Pose Estimation with Multiple Sensors[J]. arXiv preprint arXiv:1901.03642, 2019.
[4] Mascaro R, Teixeira L, Hinzmann T, et al. GOMSF: Graph-Optimization based Multi-Sensor Fusion for robust UAV pose estimation[C]//2018 IEEE International Conference on Robotics and Automation (ICRA). IEEE, 2018: 1421-1428.