摘要
On-Manifold Preintegration for Real-Time Visual-Inertial Odometry提出了IMU预积分技术并且给出了详细的数学推导过程。ORB-SLAM的作者在IMU预积分的基础之上,在ORB-SLAM中实现了VIO。因此这篇论文在一定程度上可以看作是IMU预积分技术的工程实践。
IMU预积分模型
这篇论文中的IMU预积分模型,与上一篇论文中的预积分模型基本保持一致。


Visual-Inertial ORB-SLAM
原始版本的ORB-SLAM中,系统拥有三个线程 Tracking,Local Mapping 和 Loop Closing。Visual-Inertial ORB-SLAM 将分别对这三个线程作修改,用以融合IMU信息。
Tracking
有了IMU之后,Tracking线程可以估计位姿,速度和IMU偏差,因此Tracking将会变得更加准确。
基于重投影误差和IMU预积分,建立帧与帧之间的约束关系,构造优化问题,从而得到当前帧位姿的最佳估计。
论文中根据当前是否更新了地图点,采用不同的优化方式。
1)地图点被 Local Mapping 和 Loop Closing 线程更新
此时IMU预积分误差项是建立在当前帧$j$和最近的一个关键帧$i$之间。状态估计问题建模为: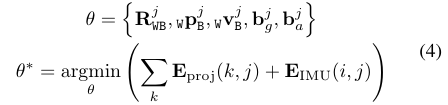
视觉误差项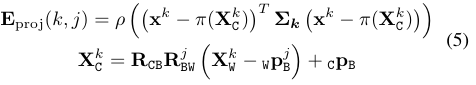
IMU误差项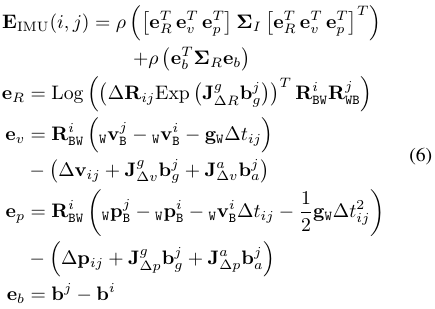
要注意的是,这里的残差项使用了Huber损失函数和马式距离。
利用g2o对公式(4)进行求解,其状态估计和Hessian矩阵将作为下一次更新的先验信息。
2) 地图点没有发生更新
此时IMU预积分误差项是建立在当前帧$j+1$和上一帧$j$之间,并利用之前已经计算得到的关于帧$j$的状态估计和Hessian矩阵建立额外的约束条件:
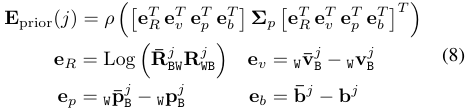
Local Mapping
对于Local Mapping线程的改动可以从下图中看出来。有了新的关键帧之后,将会对前N个关键帧进行优化,当前的关键帧(N+1)将固定不变,提供IMU预积分约束。将利用公式(5)和公式(6)建立优化问题的约束条件。
Local Mapping的另外一个功能是管理关键帧。对与local BA,如果连续关键帧之间相差小于0.5s,则进行剔除。对于full BA,如果连续关键帧之间相差小于3s,则进行剔除。
Loop Closing
由于IMU提供了尺度信息,因此全局位姿优化将从7个自由度下降到6个自由度。全局位姿优化将忽略IMU信息,因此不再优化速度和偏差,当完成全局位姿优化后,再根据矫正后的位姿对速度进行矫正。完成位姿优化后,将执行一次full BA,优化所有的系统状态,包括速度和偏差。
IMU初始化
IMU初始化对尺度,重力方向,速度和IMU偏差给出初始的估计量。这个估计量是从一系列被单目SLAM算法处理后的关键帧中估计出来的。初始化将会分为1)陀螺仪偏差估计,2)尺度和重力估计(忽略加速度偏差),3)加速度估计,并对尺度和重力方向进行修正,4)速度估计
1)陀螺仪偏差估计
陀螺仪的初始偏差估计比较简单,只需要根据ORB-SLAM求得的关键帧之间的旋转,对比利用IMU预积分模型求得的旋转,以偏差为变量,最小化两者的差值,如下图所示: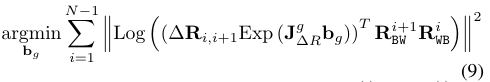
式(9)的求解将基于高斯牛顿法进行。
2)尺度和重力估计(忽略加速度偏差)
首先关注尺度如何恢复。相机位姿的坐标$p_c$与真实世界相差一个尺度$s$,可以用如下的公式表示: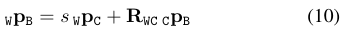
将公式(10)代入公式(3)可得: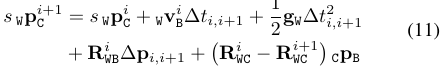
为了从等式(11)中求解尺度和重力,作者又开始了数学表演: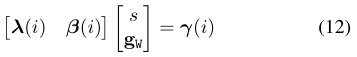

式(11)到式(12)的目的就是将速度变量$v$消除。主要思路是通过连续的三个关键帧列出两个式(11)的等式,然后利用式(3)中的速度预积分方程,将其消除。
对于$N$个连续关键帧,可以列出$N-2$个类似于式(12)的等式,其矩阵形式为$A_{3(N-2)\times 4} X_{4 \times 1 } = B_{3(N-2)\times 1}$,要求解的未知数是一个四维向量(尺度一维,重力三维),因此最少需要4个连续关键帧。
$A_{3(N-2)\times 4} X_{4 \times 1 } = B_{3(N-2)\times 1}$是一个超定方程,因此可以利用SVD来求解方程的最小二乘解。
3)加速度估计,并对尺度和重力方向进行修正
在求解式(12)时,我们忽略了加速度偏差,作者给出了忽略加速度偏差的理由。由于重力和加速度偏差比较难区分,如果直接在式(12)中加入加速度偏差,会导致其称为一个病态系统(ill-conditioned)。
而加速度偏差导致我们已经求得的重力向量是不准确的,为了求出这个加速度偏差,作者又要开始表演了。
在这里作者将重力G作为额外信息。在惯性参考坐标系下$I$中,重力的方向$\hat{g_I}=\{ 0,0,-1 \}$,而通过我们已经计算得到世界坐标系下的重力向量$g_w^* $,可以计算该重力向量的方向$\hat{g_w} = g_w^*/ \left \| g_w^* \right \| $
(刚开始一直以为世界坐标系就是惯性参考坐标系,其实并不是。最理想的世界坐标系当然是惯性参考坐标系,但是在实际中,世界坐标系往往是以第一帧的位姿作为世界坐标系的原点建立的,这与惯性参考坐标系有明显的区别)
因此就可以计算惯性参考坐标系和世界坐标系之间的旋转矩阵$R_{WI}$以及修正:

由于计算$g_w^* $时未去除加速度偏差的影响,因此要得到理想的$g_w$,需要对式(15)进行优化。假设其优化量为$\delta \theta$,则有: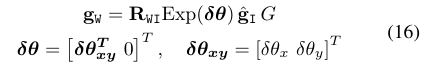
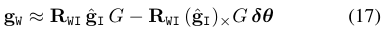
将(17)式代入(11)式,就会得到新的方程,这个方程包含了修正后的尺度$s$,重力方向的微调量$\delta \theta$和加速度偏差量$b_a$:
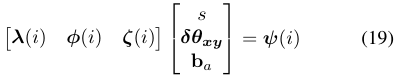

方程(19)的求解和方程(12)的求解方式类似,是一个$A_{3(N-2)\times 6} X_{6 \times 1 } = B_{3(N-2)\times 1}$的线性系统,需要至少4个连续关键帧,通过SVD求解。
4)速度估计
求得$s$, $\delta \theta$和$b_a$之后,利用式(18)和式(3),即可求解每个关键帧的速度$v$。
5)偏差重估计
当重定位模块完成了重定位之后,会利用式(9)对陀螺仪偏差重新估计。
加速度偏差用式(19)重新估计,只不过此时不需要再估计尺度和重力。
参考文献
Visual-Inertial Monocular SLAM with Map Reuse