Why VIO
首先我们先简单回顾一下为什么要做VIO,以及为什么要做VIO初始化。
我们知道单目相机在做SLAM的时候是缺乏实际的尺度信息的,而且尺度还会产生漂移。如果缺乏实际的尺度信息,此时的定位信息将很难进行实际的应用。在面对一些极端环境的时候或者突然运动过快的时候,视觉还可能直接跟丢。还有一点就是,纯视觉的SLAM系统如果不做特殊处理,是无法知道惯性坐标系的,视觉SLAM出的pose大多都是基于第一帧为世界坐标系建立的,所以就有可能出现车明明是在地上开,出的轨迹看上去在朝天上飞。最后一点就是视觉SLAM是无法得到一个比较准确的速度的。而这个速度对于控制和规划来说是非常重要的。
那这些问题要如何解决呢?VIO就是一种非常优美的解决方式,因为IMU可以提供物理世界的尺度,短时间内也能提供比较准确的位姿估计,还能估计出惯性坐标系。这种互补的性质,让VIO在近几年得到了极大的关注。
当然了,VIO这么多的好处不是白来的,是需要付出很多努力的。首先就是初始化这件事情。VIO初始化要干个啥,就是把我们之前所说的视觉SLAM所缺的东西全部都先估计出来,包括尺度,重力方向,速度。还有通过视觉SLAM帮助IMU去搞定bias。如果这些东西一开始估计的很差,那整个系统的准确性会急剧下降。基于滤波的很可能很快就发散得很远了,基于非线性优化的可能经常会陷入局部最优解。
那为什么VIO的初始化会这么难。首先第一点就是,在单目视觉SLAM中,绝对尺度和速度都是无法计算出来的。而要计算尺度和速度,系统就要做非匀速的运动。而一旦动起来,重力方向相对于当前相机坐标系的方向就成了一个未知量,而我们知道IMU加速度计的读数是受重力影响的,如果重力方向未知,IMU就无法估计位姿了。而且就算是计算出了重力方向,隐藏在IMU的尺度信息通常又会受到噪声和Bias的影响,如果处理不好,尺度也会估的不准。
在正式进入论文梳理之前,我们再次明确一下VIO初始化到底要解决哪些问题。首先是要估计尺度信息,其次是重力向量,包含方向和大小,之后是每个pose的速度,最后是陀螺仪和加速度计的初始bias。有些牛逼一点的VIO初始化,还会顺带把相机和IMU之间的相对位姿关系给估计出来,这样就不需要预先对相机和IMU进行外参标定。最后一点就是要明确,VIO初始化成功的标准到底是什么。
预积分
On-Manifold Preintegration for Real-Time Visual-Inertial Odometry
那接下来进入我今天要分享的第一篇paper。其实这一篇不是VIO的初始化,而是VIO中最基本的内功心法-预积分。相信熟悉VIO的同学都非常熟悉这篇Paper,特别是基于非线性优化的VIO。预积分这种思路就感觉是武林绝学中的内功心法,OKVIS,VINS-Mono,VI-ORB,VI-DSO都是基于预积分的思想来实现VIO的。在这里快速地过一遍IMU预积分的论文,回顾一下VIO初始化中需要用到的关于预积分的知识点。
首先我们看一下从IMU中拿到的数据到底是什么。它包含角速度和加速度两部分,它们都是基于IMU坐标系。在VIO中通常会存在这么几个坐标系,一个是世界坐标系,一个是相机坐标系,一个是IMU坐标系,同一时刻下相机坐标系和IMU坐标系是刚体连接的,因此相机和IMU之间会有一个包含旋转和平移的外参。世界坐标系通常为第一帧图像的相机坐标系。除此之外,还有一个惯性坐标系,在惯性坐标下,重力只作用在Z轴上。在VIO中,通常完成初始化之后会把世界坐标系转正,其世界坐标系和惯性坐标系保持一致。我们再仔细看一下等式(27)和等式(28),左边的角速度和加速度是我们可以直接从IMU中拿到的度数,但它与物体实际的运动物理量还存在一个转换关系。角度速会受到bias和噪声的影响。加速度除了受到bias和噪声的影响,还会受到重力的影响。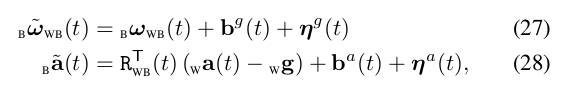
那么我们怎么从IMU的读数中估计位姿呢?这就涉及到了运动学模型。我们知道角速度积分得到角度,加速度积分得到速度,速度积分得到平移量。而IMU的读数是离散的,因此会采用累加求和的方式,也就是公式(30),这里的角速度和加速度都是物体实际的运动物理量。因此把上一页的等式带入,可以得到旋转,速度,平移与IMU读数之间的关系。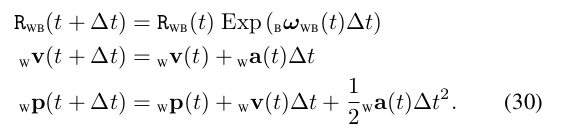
我们还要注意一个问题就是,相机的采样频率是明显低于IMU的采样频率的,相机一般在几十HZ,而IMU可以达到几百HZ,而在SLAM中我们通常是求解每个图像时刻的pose,因此对两个图像之间的IMU观测进行累加,可以得到i帧和j帧之间的位姿和速度关系。但是在等式(32)中有个非常让人恼火的事情,就是在更新速度的时候,需要每个IMU时刻的世界坐标系下的旋转,在更新平移时,需要每个IMU时刻世界坐标系下的速度和旋转。要知道IMU有几百hz的频率,每次都要更新所有状态显然是不合理的。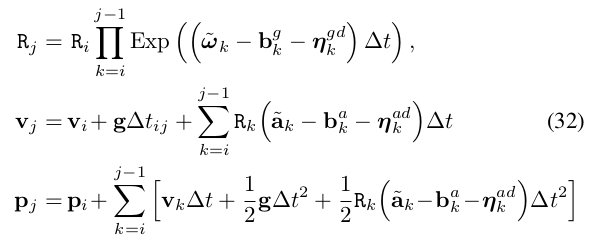
这个时候,预积分就从天而降,开始拯救世人。我们可以把目光投射到这个公式(33)上,等式的最右边就是预积分量,它与世界坐标系下的旋转和速度是解偶的,只需要通过IMU的读数和前一时刻的预积分量就可以更新当前的预积分量。当然了公式(33)还是有一片乌云的,那就是在bias变化的时候需要重新累加计算所有的IMU数据得到预积分量,为了降低这个计算量,可以通过公式(44),利用bias的变化量来更新预积分量。这个公式(44)在VIO初始化中起到了非常重要的作用,因为它建立预积分量和bias的变化量之间的线性关系。更多更详细的推导可以参考论文和论文的附录。也可以参考很久之前写过的一篇预积分的博客.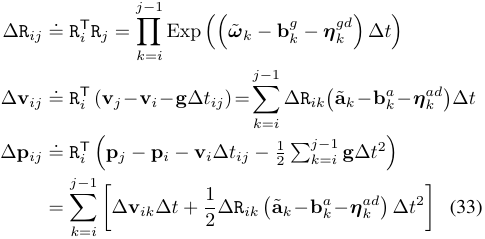
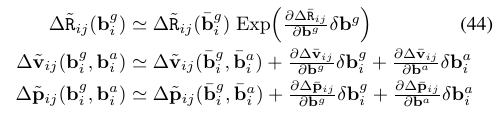
Paper 1
Monocular Visual-Inertial State Estimation with Online Initialization and Camera-IMU Extrinsic Calibration (2017, HKUST)
这篇论文是2017年,港科大沈老师组里出的一篇paper。要解决的就是VIO的初始化问题。这篇论文的VIO初始化可以求解出尺度,重力,速度和相机和IMU之间的内外参,但是忽略了bias的估计,
第一步,就是要求解相机和IMU之间的旋转。公式(4)是标准的手眼标定公式。如果不熟悉手眼标定算法,可能一时不能理解这个转换关系。这里我暂时先不展开讲,因为到后面的某一篇论文还会再次用到,到那个地方再进行一步一步的推导。我们回到公式(4),$R^{b_k}_{b_{k+1}}$可以通过预积分得到,$R^{c_k}_{c_{k+1}}$可以通过5点法计算。公式(4)里面是旋转矩阵,我们用四元数重写公式(4)得到公式(5),把公式(5)的右边减到左边,再用左乘和右乘矩阵来代替四元数,就可以得到公式(5)的下半部分。把多个时刻的旋转都叠在一起,可以构造一个超定方程。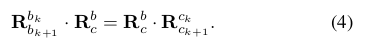
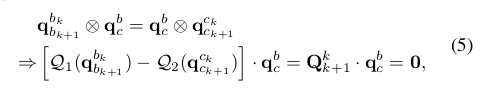
第二步就有点猛了,要把速度,重力,特征点深度,相机和Camera之间的平移量干出来。这就构造了这里待估计的$X$状态量,也就是所有需要估计出来的变量。我们来看公式(11),第二项是通过IMU预积分的速度和平移建立的约束项,第三项是视觉观测项,观测误差是其在归一化平面的坐标差。
我们把IMU观测项和视觉观测项联立在一起,可以得到一个线性方程,如公式(21)。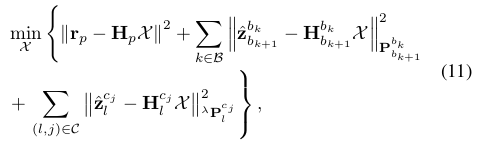
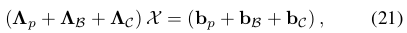
简单总结下这篇论文的初始化方式。它其实采用的是一种有点类似于紧耦合的方式,因为视觉特征点的深度、相机的平移是与重力、速度一起估计出来的。所以如果特征点的深度分布的范围比较大的话,很容易估计的不够准确。另外忽略bias很容易会引入误差。目前这种初始化方式除了外参旋转的估计方式还保留在VINS-Mono的代码中,其他已经被舍弃了。
Paper 2
Visual-Inertial Monocular SLAM With Map Reuse (2017 VI-ORB)
这是ORB-SLAM的作者在做VIO时提出的一种初始化方式。这种初始化方式可以理解为是松耦合的方式。首先视觉SLAM先进行初始化,得到了三维空间中一系列的相机位姿和地图点。而在这个过程中,IMU持续进行预积分,得到每两个关键帧之间的预积分量。之后再把视觉初始化得到的相机位姿和预积分量进行对齐。在VI-ORB中初始化中估计了尺度,重力,速度,陀螺仪和加速度计的bias,而没有估计外参。
第一步是进行陀螺仪bias的估计。根据视觉初始化得到的相机的旋转,通过外参,我们可以转化为IMU的旋转。而通过连续两帧的IMU旋转可以和预积分量建立约束。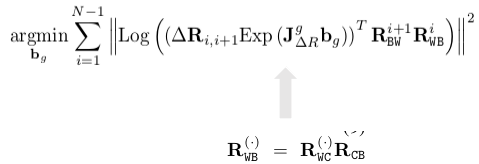
第二步是进行尺度和重力的估计,这一步忽视加速度计bias,至于这一步为什么要忽略加速度计的bias,我们在下一步再讲。我们现在把目光注意到公式(10)上,它描述了世界坐标系下相机的平移,如何通过尺度和外参变换成世界坐标系下IMU的平移。然后再结合预积分的关系,也就是把预积分关系中的IMU的平移利用等式(10)替换为相机的平移。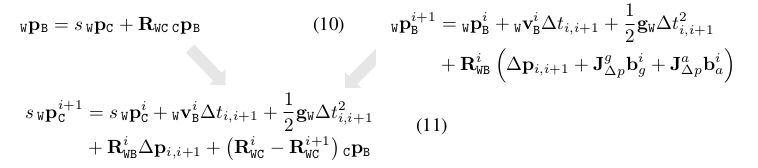
由于在这一步,只估计尺度和重力,而不估计速度,因此可以在列一个i+2时刻的等式(11),然后通过速度的预积分关系,将速度项从等式(11)中消去。此时即可得到等式(12)。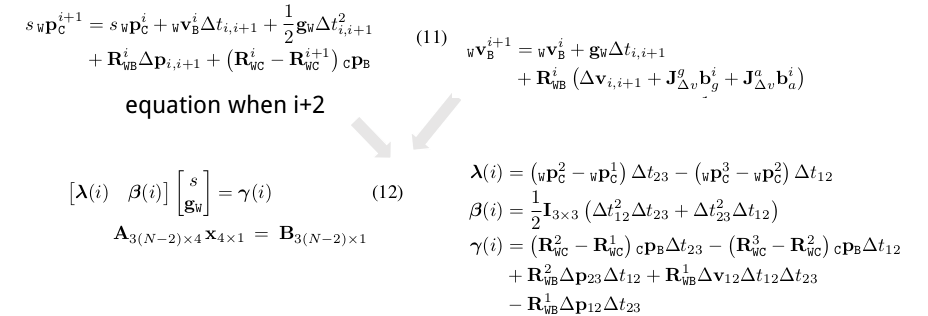
对于$N$个连续关键帧,可以列出$N-2$个类似于式(12)的等式,其矩阵形式为$A_{3(N-2)\times 4} X_{4 \times 1 } = B_{3(N-2)\times 1}$,要求解的未知数是一个四维向量(尺度一维,重力三维),因此最少需要4个连续关键帧。
$A_{3(N-2)\times 4} X_{4 \times 1 } = B_{3(N-2)\times 1}$是一个超定方程,因此可以利用SVD来求解方程的最小二乘解。
第三步是进行加速度计bias的估计,以及对尺度和重力方向进行进一步修正。因为加速度计的bias相比于重力来说,从量级上是非常小的,因此如果放到等式(12)中,很可能是不可观的,也就是很可能导致A矩阵是一个病态矩阵。因此没有放在上一步去求解。在这里作者将重力G作为额外信息。在惯性参考坐标系下$I$中,重力的方向$\hat{g_I}=\{ 0,0,-1 \}$,而通过我们已经计算得到世界坐标系下的重力向量$g_w^* $,可以计算该重力向量的方向$\hat{g_w} = g_w^*/ \left \| g_w^* \right \| $
世界坐标系往往是以第一帧的位姿作为世界坐标系的原点建立的,这与惯性参考坐标系有明显的区别,所以求解出的重力向量$g$的方向与$\hat{g_I}=\{ 0,0,-1 \}$是有区别的。
因此就可以计算惯性参考坐标系和世界坐标系之间的旋转矩阵$R_{WI}$以及修正: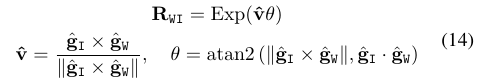

由于计算$g_w^* $时未去除加速度偏差的影响,因此要得到理想的$g_w$,需要对式(15)进行优化。假设其优化量为$\delta \theta$,则有: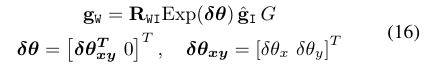
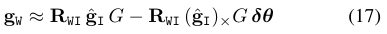
将(17)式代入(11)式,就会得到新的方程,这个方程包含了修正后的尺度$s$,重力方向的微调量$\delta \theta$和加速度偏差量$b_a$: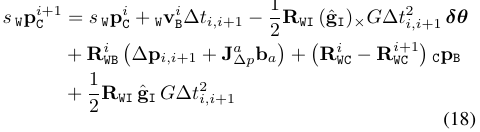
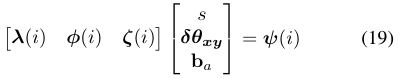
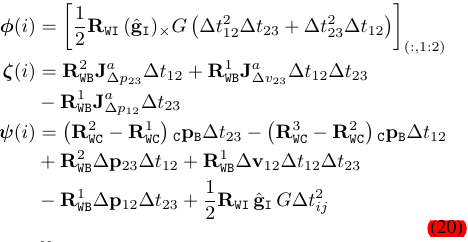
方程(19)的求解和方程(12)的求解方式类似,是一个$A_{3(N-2)\times 6} X_{6 \times 1 } = B_{3(N-2)\times 1}$的线性系统,需要至少4个连续关键帧,通过SVD求解。
Paper 3
Robust Initialization of Monocular Visual-Inertial Estimation on Aerial Robots (2017, HKUST)
看到 VI-ORB 的初始化方式有点厉害,港科随后也更新了一波VIO的初始化方式。也就是目前在VINS-Mono中使用的方式。
总的来说,和VI-ORB是大同小异的。首先是先对视觉部分进行初始化,然后估计陀螺仪的bias,之后估计重力,尺度和速度。这里并没有像VI-ORB一样把速度项给消去,而是选择将其作为未知变量估计出来。最后也是利用重力的norm对重力,尺度和速度进行refine。
这部分就不展开讲了,可以参考之前分析 VINS-Mono 时候写过的一篇关于初始化的博客。VINS-Mono中的VIO初始化
由于VINS-Mono在初始化的时候忽略了加速度计的bias,看上去好像比VI-ORB要弱一些。所以有意思的是,这篇Paper最后还特意解释了一下为啥不估计加速度计的bias。
1.他们通过仿真结果证明了,如果运动不够剧烈(smooth motion),加速度计的bias是很难被观测出来的
2.其次忽略加速度计的bias对估计其他初始值的影响并不大。
3.加速度计的bias是可以通过之后的VIO紧耦合优化,慢慢被估计出来。
4.在VI-ORB中,加速度计bias的收敛需要好几秒,而且没有一个很好的判定条件来判断加速度计bias的估计是否正确。
Paper 4
Online Initialization and Automatic Camera-IMU Extrinsic Calibration for Monocular Visual-Inertial SLAM (2018, Peking)
这篇paper是发表在2018年的ICRA上,乍一看题目还是很叼的,要把VIO初始化中所有的状态量都估计出来,包括相机和IMU的内外参。但是仔细一读,唉,原来发篇顶会也不是什么难事。
第一步是估计相机和IMU的旋转外参和陀螺仪的bias。
这篇Paper把Paper 1中估计旋转的外参方式抄了一遍,然后把Paper 2中估计陀螺仪bias的方式再抄一遍。因为估计旋转外参需要依赖陀螺仪bias的估计(为了得到更准确的IMU预积分),而估计陀螺仪的bias又会依赖于旋转外参。因为这种蛋生鸡鸡生蛋的相互依赖关系,这里提出了旋转外参估计和陀螺仪bias估计迭代着来做的方法,可以最终使得旋转外参和陀螺仪bias的估计都收敛到正确的值上。嗯,好像还有点创新。
第二步是估计重力、尺度、外参平移。
这里又几乎把VI-ORB中的第二步抄了一遍,略微有点不同的是,VI-ORB中的第二步只估计的重力和尺度,这里把平移的外参给加上了,因此待估计的状态量多了3维。
第三步是估计加速度计的bias,并对重力、尺度、外参平移进行refine。
与VI-ORB的第三步类似。
总结
读完这几篇文章,感觉从理论上,基于预积分的VIO初始化问题已经解决了,但实际上工程运用的时候还是有很多坑的。比如某些轴上的运动激励不够要怎么处理,在尺度完全未知的情况下如何判断VIO初始化给出的尺度就一定是准确的,也包括港科在论文中提到的,如何判定加速度计bias的初始化结果是可信的。这些问题可能需要在我自己做完VIO初始化之后再跟大家交流。
参考文献
- On-Manifold Preintegration for Real-Time Visual-Inertial Odometry
- Visual-Inertial Monocular SLAM With Map Reuse
- Robust Initialization of Monocular Visual-Inertial Estimation on Aerial Robots
- Online Initialization and Automatic Camera-IMU Extrinsic Calibration for Monocular Visual-Inertial SLAM
- SLAM 论文阅读和分类整理