DSO
DSO,又名稀疏直接法。刚问世的时候,在 SLAM 领域中就像是一股清流。因其炫酷的可视化效果,火遍朋友圈。那到底何为直接法,那得从特征点法说起。
特征点法,通常就是三板斧。首先是对图像提取图像特征(如ORB,FAST等)。其次就是在两帧图像之间建立特征匹配关系。这一步通常有两种方法,第一种为描述子匹配(如ORBSLAM),第二种为光流匹配(如VINS)。最后就是求解位姿。根据已知的条件,可以使用对极约束(2D-2D),PnP、BA(3D-2D),ICP(3D-3D)等方法。
而直接法,只需要图像之间的灰度误差关系,即可完成位姿求解。简直就是耍流氓。
因此,简单来讲,特征点法,优化目标是使得特征匹配时的几何误差(坐标误差)最小,通常称为 geometric error,因此非常依赖于特征的匹配是否正确。而直接法,优化目标是图像间的灰度误差最小,通常称为 photometric error,因此非常依赖于图像间的灰度一致性。直接法更加详细的基本概念可以先参考十四讲。
DOS论文洋洋洒洒十几好页,其中最关键的就是下面的残差函数。接下来将详细讲解这个残差函数。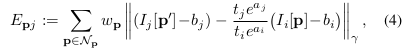
(1)$p \in N_p$ 即为下图的选点策略。选取8个点方便SSE加速。
(2)$w_p$表示权重,计算方式如下。(这个c到底是个啥?)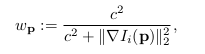
(3)$t_i, t_j$分别表示 $i$ 和 $j$ 时刻的相机曝光时间。$a_i, b_i, a_j, b_j$表示亮度转移函数参数(brightness transfer function parameters)。因此(4)中相减的两项,即为光度修正后的图像灰度值。
(4)$p$ 和 $p’$ 分别表示像素点在$i$ 和 $j$ 时刻的坐标,其满足以下转换关系。其中 $d_p$ 表示逆深度。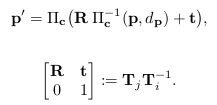
因此,每个关键帧时刻,对于滑窗内的关键帧,DSO会建立如下的优化函数,优化变量为滑动窗内每一时刻的帧Pose,点的逆深度,当然也可以再优化内参、曝光时间和亮度转移函数。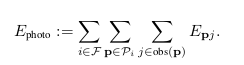
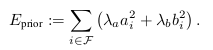
在DSO中,选择哪些点加入到滑动窗口中进行优化,对最终的结果将会产生决定性的影响,DSO中的稀疏二字,代表着在每个图像帧中,将会有选择性的选择某些像素,而不是全部像素。对于直接法的优化问题,将产生如下的雅可比矩阵。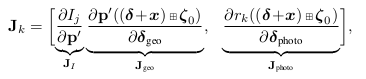
可以看到雅可比矩阵的第一项即为像素梯度,因此对于每个图像帧,只有那些具备梯度的像素,才具备被优化的条件。这是直接法选点的第一个条件。
其次在优化地图点的过程中,当调整地图点的逆深度,其投影到其他图像帧时,是在极线上变化的,如果该极线上的像素值都是一样的,那么直接法优化的残差函数将不产生任何变化。这是直接法选点的第二个条件,即极线上必须是有像素变化的。
为了得到更加准确的优化结果,选点时还需要使其均匀分布在图像中,这是直接法选点的第三个条件。
关于 First Estimate Jacobians 和 Marginalization 的内容就不展开说了,[1][2][3]都讲的非常透彻,以后有机会再写写自己的理解。
双目DSO
单目SLAM在本质上是存在缺陷的,无法估计实际尺度以及在运行过程中尺度会发生漂移,这些问题在实际的应用中是非常致命的,因此自然而然地就会想到用双目来做DSO。
双目DSO中提出了两个概念。
Temporal Multi-View Stereo
这部分其实和单目DSO相比,残差的建立和待优化的变量都是没有区别的,只是从1个相机图像的直接法约束,增加到2个相机图像的直接法约束。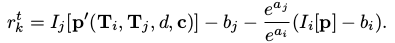
Static Stereo
这部分是双目相机之间的直接法约束。由于双目相机之间的外参是已知的,因此不需要估计相机之间的相对位姿关系($ T_{ji} $)。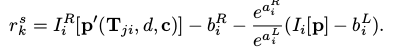
通过将 Temporal Multi-View Stereo 和 Static Stereo 组合在一起,即可得到双目DSO的优化目标函数。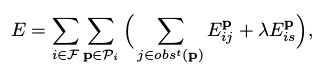
相比于单目DSO,双目DSO还有一个改进点就是可以得到候选像素的在三维空间中的初始深度,而不再像单目DSO一样,采用随机值。具体的做法就是通过 NCC 得到双目相机之间的像素匹配,然后根据双目相机的基线得到深度估计。
总体开说,双目DSO在单目DSO的基础上,并没有什么亮眼的创新点,但由于传感器从单目升级到了双目,在 KITTI 和 Cityscapes 数据集上吊打各路英豪。
这里有几个双目DSO的开源版本。
https://github.com/HorizonAD/stereo_dso
https://github.com/JingeTu/StereoDSO
接下来再进一步学习。
VI-DSO
双目SLAM理论上是非常优美的,但相较于单目SLAM,需要处理双倍的图像数据,因此计算量也是双倍的。针对单目SLAM无法估计尺度的问题,还有一个更加优美的方式就是加入IMU。
VIO也是近几年SLAM研究领域的热门。DSO也在2018年的ICRA上发表了 DSO+IMU 的论文。
与很多VIO类似,VI-DSO的优化目标函数包含视觉残差项和IMU残差项两部分。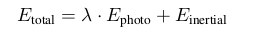
视觉残差项$E_{photo}$与单目DSO是一模一样的,就不再重复了。
由于视觉残差项计算的是图像的亮度误差,而IMU残差项计算的是位姿误差,两者并不在一个量纲上,在VI-ORB中和VINS中,是通过强行增加一个视觉残差项的协防差,使得视觉残差项通过这个协防差变为一个无量纲的马氏距离估计。
而VI-DSO中则更加暴力,直接乘上了一个权重。
IMU残差项也是遵循了IMU预积分的那一套理论。IMU预积分部分,可以详细参考[4].
除了优化目标函数,VIO还有一个很重要的部分就是初始化。
论文中说自己的创新点在于把尺度和重力方向都作为优化问题的状态量,进行优化。具体的步骤如下:
1.和单目一样进行视觉部分的初始化
2.利用40个加速度计的观测,计算重力方向,作为后续优化问题的初值。
3.bias的初值为0,尺度的初值为1。
有了初始值之后,即可构造优化问题,对上述的状态量进行联合优化。
VI-DSO的初始化部分讲的并不详细,甚至有点不负责任,可是,谁让人家是大佬呐。。。
构造优化问题时, VI-DSO 构造了两个坐标系,一个是 DSO坐标系,用来描述图像视觉观测项,一个是 metric坐标系,用来描述IMU观测项,两个坐标系之间存在一个旋转和尺度的差异,可以表示为
$$ T_{m\_d} \in \{T \in SIM(3) \ | \ \mathrm{translation(T)} = 0\} $$
每新加一个关键帧,需要新增加的优化变量为此时相机在DSO坐标系下的相机位姿,速度,IMU的偏差、光度矫正参数以及空间中三维点的逆深度,即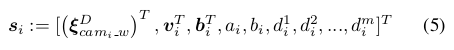
而整个滑动窗口内的优化问题来说,优化的变量还有相机内参,$ T_{m\_d} $,即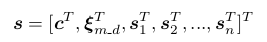
由于在建立视觉残差项用的时DSO坐标系下的相机位姿,而在建立IMU残差项的时候用的是metric坐标系下的IMU位姿,两者之间存在一个转换关系,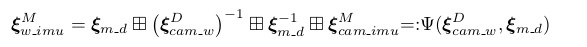
为了简化IMU残差项中H矩阵的表示,VI-DSO中定义了一个临时变量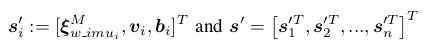
其对应的H矩阵为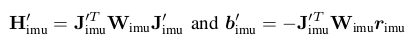
$H’_{imu}$ 和 $H_{imu}$之间的转换关系为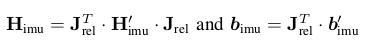
$\mathrm{J_{rel}}$分为两部分,一部分是imu残差项对$T^D_{cam_i\_w}$进行求导,另一部分是imu残差项对$T_{m\_d}$求导。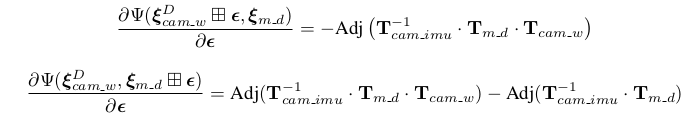
其实这里明明可以直接推导雅可比,偏偏要硬搞一个转换关系,被绕得一脸懵逼。至于$\mathrm{J_{rel}}$的推导,嗯…
为了使得 Marginalization 更有效,VI-DSO提出了一种新策略叫做 Dynamic Marginalization。
VI-DSO构造了三种不同的先验项$\mathrm{M_{visual}},\mathrm{M_{half}},\mathrm{M_{curr}}$。
首先定义$\mathrm{G_{metric}}$为IMU残差项,$\mathrm{G_{visual}}$为视觉残差项,在每次滑窗优化的时候,总是构造优化问题$\mathrm{G_{ba}} = \mathrm{G_{metric}} \cap \mathrm{G_{visual}} \cap \mathrm{M_{curr}}$。
当需要 marginalization 关键帧 $i$ 的时候,对优化问题 $\mathrm{G_{visual}} \cap \mathrm{M_{visual}}$ 进行边缘化得到 $\mathrm{M_{visual}}$,对优化问题 $\mathrm{G_{ba}}$ 进行边缘化得到 $\mathrm{M_{curr}}$,对优化问题 $\mathrm{G_{metric}} \cap \mathrm{G_{visual}} \cap \mathrm{M_{half}}$ 进行边缘化得到 $\mathrm{M_{half}}$。
每次进行边缘化的时候,会根据尺度的变化来选择到底使用哪一种先验项。具体的算法流程如下图
在论文附录中也通过实验证明了Dynamic Marginalization的有效性。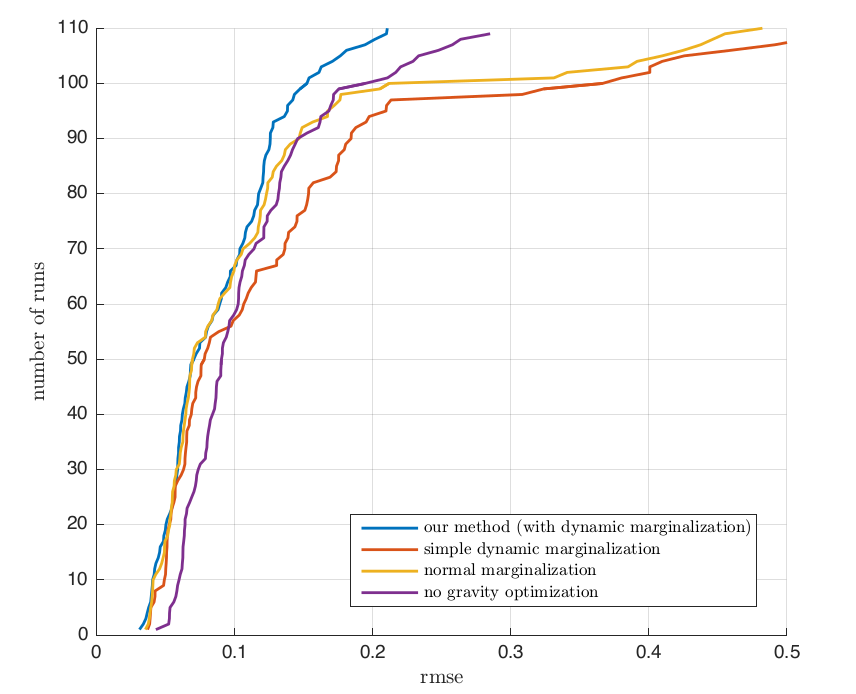
下面进入瞎说环节。为什么要搞个这么复杂的Dynamic Marginalization,感觉上是因为先验项虽然可以保留那些被Marginalization掉的约束信息,但是终究是会产生损失的。特别是在边缘化IMU约束的时候,由于尺度信息完全有IMU来提供,因此当边缘化IMU信息的时候很有可能会导致尺度的漂移。
所以Dynamic Marginalization建立了三种不同的先验项 $\mathrm{M_{visual}},\mathrm{M_{half}},\mathrm{M_{curr}}$。$\mathrm{M_{curr}}$包含了完整的边缘化信息,但由于累积的信息越来越多,信息越来越陈旧,反而会干扰尺度估计的准确性。因此在适当的时候,需要丢弃残旧的先验项$\mathrm{M_{curr}}$,更换为比较新的先验项$\mathrm{M_{half}}$。
ps.好想VI-DSO能够开源啊
LDSO
虽然LDSO的作者是大名鼎鼎的高翔,但是我还是想说一句,这篇文章有点。。。
这篇文章大概可以用三句话来概括。
1.在DSO选点策略的基础上,判断其是否符合角点性质,如果符合角点性质,则计算orb描述子并将该帧打包成词袋。
2.如果词袋搜索到候选帧,则计算当前帧和候选帧之间的sim3变换。如何在当前帧中,某一个点已经计算出了三维坐标,则计算三维坐标的残差。如果某个点还没有计算出三维坐标,则将候选帧中的三维点投影到当前帧中,计算重投影误差。如下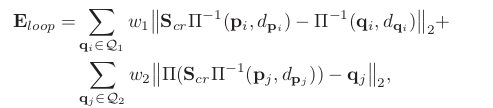
3.有了当前帧和回环帧之间的sim3关系之后,即可进行posegraph优化。为了防止posegraph优化干扰到滑动窗口内的优化结果,直接将滑动窗口内的帧固定住,优化历史上更老的帧。
LDSO代码已经开源。抽空再继续学习细节,说不定有骚操作。
https://github.com/tum-vision/LDSO。
参考文献
- DSO详解
- 如何理解SLAM中的First-Estimates Jacobian
- DSO 中的Windowed Optimization
- On-Manifold Preintegration for Real-Time Visual–Inertial Odometry