VINS-Mono中的VIO紧耦合方案

摘要

VIO 紧耦合方案是每个VIO系统最重要的组成部分，本篇博客将结合论文和相关代码，对 VINS-Mono 的紧耦合方案作详细分析。

概述

VIO 紧耦合方案的主要思路就是通过将基于视觉构造的残差项和基于IMU构造的残差项放在一起构造成一个联合优化的问题，整个优化问题的最优解即可认为是比较准确的状态估计。
为了限制优化变量的数目，VINS-Mono 采用了滑动窗口的形式，待估计量均为滑动窗口内的状态变量，如下图所示。

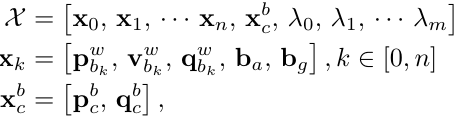
其中需要注意的是 VINS-Mono 中对于地图点的参数化形式。 VINS-Mono 用第一次观测到该地图点的相机坐标系下的逆深度来表示一个地图点，即上图中待估计变量 λ。其总数 m 为滑动窗口内能够观测到的所有地图点的数目。
VINS-Mono 中构造了三个残差项。第一项为先验项，第二项是视觉残差项，第三项是 IMU 残差项，如下图所示。

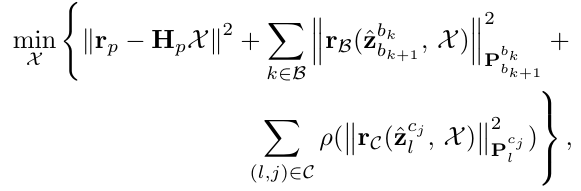
残差项的构造和求解都在函数 void Estimator::optimization() 中。
滑动窗口内所有待优化变量都保存在一个数组中，如下所示。VINS-Mono 在整个运行过程中的最终目的，就是要通过构造残差项，优化得到准确的状态估计量。

class Estimator{
    Vector3d Ps[(WINDOW_SIZE + 1)]; //平移
    Vector3d Vs[(WINDOW_SIZE + 1)]; //速度
    Matrix3d Rs[(WINDOW_SIZE + 1)]; //旋转
    Vector3d Bas[(WINDOW_SIZE + 1)]; //加速度偏差
    Vector3d Bgs[(WINDOW_SIZE + 1)]; //陀螺仪偏差
}

接下来我们来着重分析下这三个残差项是怎么构造的。

IMU 残差项

首先来看 IMU 的残差项，如下图所示。

IMU预计分的具体细节和公式推导就不展开讲了，主要可以参考文献[1]和文献[2]。我们直接给出IMU预积分的处理流程。对于每个IMU数据，需要处理三件事情。第一，更新当前的预积分量。第二，更新IMU残差的协防差矩阵。第三，更新IMU残差对于bias的雅克比矩阵。明确了这三件事情之后，我们再来看看 VINS-Mono 是怎么做这三件事情的。

VINS-Mono 中处理 IMU 数据的入口是void Estimator::processIMU(double dt, const Vector3d &linear_acceleration, const Vector3d &angular_velocity)。在void Estimator::processIMU(...)函数中，有个很关键的函数调用就是pre_integrations[frame_count]->push_back(dt, linear_acceleration, angular_velocity)。在这个函数中，VINS-Mono把上面提到的三件重要的事情全部都做了。滑动窗口内所有预积分的信息保存在IntegrationBase *pre_integrations[(WINDOW_SIZE + 1)]。

class IntegrationBase{
    Eigen::Vector3d delta_p; //平移预积分
    Eigen::Quaterniond delta_q; //旋转预积分
    Eigen::Vector3d delta_v; //速度预积分
    Eigen::Matrix<double, 15, 15> jacobian, covariance; //雅可比矩阵和协方差矩阵
}

首先是更新预积分量。
需要注意的是，VINS-Mono 在代码中采用了中值积分的方式，与论文中的欧拉积分不同。
更新预积分的公式为：

其次是更新协方差矩阵和雅可比矩阵。
在误差传播的过程中有这样一种性质，如果能找到状态量的递推公式 $\delta z_{k+1} = F \delta z_k + G n_k$
则有协方差 $P_{ik+1}$ 和 IMU 残差对于bias的雅可比矩阵 $J_{ik+1}^{b}$ 的递推更新公式：
$$
P_{ik+1} = F_{k}P_{ik}F_{k}^T + G_{k}P_nG_{k}^T
\\
J_{ik+1}^{b} = F_{k}J_{ik}^{b}
$$

其中 $P$ 表示协方差，$J$ 表示IMU预积分残差对于bias的雅可比矩阵。
在 VINS-Mono 中采用了中值积分的方式计算预积分，递推公式如下：

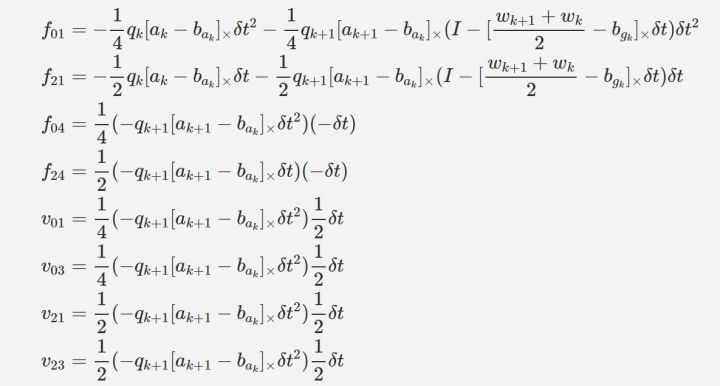
之前一直纠结于 $F$ 和 $G$ 的形式为什么在 VINS-Mono 中和 Foster 的预积分论文中的形式不一样。Foster 的预积分论文中给出了 $F$ 和 $G$ 的完整推导过程。但是 VINS-Mono 直接给出了 $F$ 和 $G$ 的具体形式，并没有给出推导过程。从直观的角度来看，当误差通过 $\delta z_{k+1} = F \delta z_k + G n_k$ 进行传播时，$z_k$ 和 $n_k$ 的变化是通过雅可比矩阵来传播的，因此 $F$ 是当前时刻的状态量 $z_{k+1}$ 对上一时刻状态量 $z_k$ 的雅可比矩阵，$G$ 是当前时刻的状态量 $z_{k+1}$ 对上一时刻误差项 $n_k$ 的雅可比矩阵。参考知乎上的一个答案，这部分的推导应该可以从参考文献[2]中找到。待进一步学习。

VINS-Mono 关于 IMU 误差项的定义在 imu_factor.h 中。这里在提一下 Ceres 对于残差的计算，如下

Eigen::Matrix<double, 15, 15> sqrt_info = Eigen::LLT<Eigen::Matrix<double, 15, 15>>(pre_integration->covariance.inverse()).matrixL().transpose();
residual = sqrt_info * residual;

为了保证 IMU 和 视觉參差项在尺度上保持一致，一般会采用与量纲无关的马氏距离，即 $e^TP^{-1}e$ ，但这明显与 VINS-Mono 代码中不一致。这是因为ceres只接受最小二乘优化, 也就是 $e^Te$ 。为了将欧式距离转换为马氏距离，首先得把 $P^{-1}$ 做LLT分解，即 $P^{-1}=LL^T$ , 因此有 $e^TP^{-1}e = e^TLL^Te = (L^Te)^T(L^Te)$ , 令 $e′=L^Te$ 作为新的优化误差, 这样就能用ceres求解了。Eigen::LLT<Eigen::Matrix<double, 15, 15>>(pre_integration->covariance.inverse()).matrixL().transpose()这一行代码其实就是代表将$P^{−1}$作LLT分解，然后取$L^T$。

视觉残差项

视觉的残差项在 SLAM 系统中都大同小异，但在 VINS-Mono 中要注意两点。第一是 VINS-Mono 中对于地图点的参数化形式，即逆深度的形式。第二是残差的计算。残差的计算给出了两种形式，第一种是在归一化平面上的重投影误差，这种误差更常见，也更好理解。第二种是把归一化平面上的重投影误差投影到Unit sphere的误差。论文中给出的是第二种，而代码中两种误差都保留了，并用宏UNIT_SPHERE_ERROR进行控制。误差计算公式是写成这样的：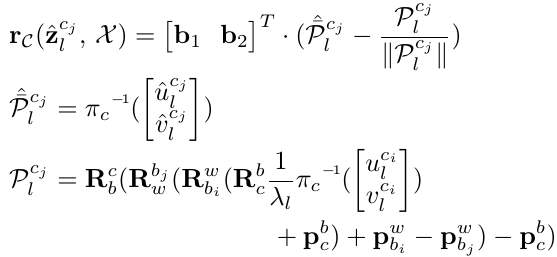

代码是写成这样的：

    //i时刻相机坐标系下的map point的逆深度
    double inv_dep_i = parameters[3][0];
    //i时刻相机坐标系下的map point坐标
    Eigen::Vector3d pts_camera_i = pts_i / inv_dep_i;
    //i时刻IMU坐标系下的map point坐标
    Eigen::Vector3d pts_imu_i = qic * pts_camera_i + tic;
    //世界坐标系下的map point坐标
    Eigen::Vector3d pts_w = Qi * pts_imu_i + Pi;
    //在j时刻imu坐标系下的map point坐标
    Eigen::Vector3d pts_imu_j = Qj.inverse() * (pts_w - Pj);
    //在j时刻相机坐标系下的map point坐标
    Eigen::Vector3d pts_camera_j = qic.inverse() * (pts_imu_j - tic);
    Eigen::Map<Eigen::Vector2d> residual(residuals);
#ifdef UNIT_SPHERE_ERROR 
    residual =  tangent_base * (pts_camera_j.normalized() - pts_j.normalized());
#else
    double dep_j = pts_camera_j.z();
    residual = (pts_camera_j / dep_j).head<2>() - pts_j.head<2>();
#endif

把归一化平面上的重投影误差投影到Unit sphere上的好处就是可以支持所有类型的相机。对于成像在平面上的相机，直接计算投影在x轴和y轴坐标的差是没有问题的，但是如果是成像在曲面上的相机，直接计算投影在x轴和y轴坐标的差往往是不够准确的，所以要转换到Unit sphere。这部分的实际效果还有待进一步验证。

在最新版本的 VINS-Mono 中，还添加了对 imu-camera 时间戳不完全同步和 Rolling shutter 相机的支持。主要的思路就是通过前端光流计算得到每个角点在归一化的速度，根据 imu-camera时间戳的时间同步误差和Rolling shutter相机做一次rolling的时间，对角点的归一化坐标进行调整。
这部分代码在projection_td_factor.h文件中。其实这里面最关键的代码就两行。

pts_i_td = pts_i - (td - td_i + TR / ROW * row_i) * velocity_i;
pts_j_td = pts_j - (td - td_j + TR / ROW * row_j) * velocity_j;

其中pts_i是角点在归一化平面的坐标，td表示imu-camera时间戳的时间同步误差，是待优化项。TR表示Rolling shutter相机做一次rolling的时间。因为在处理imu数据的时候，已经减过一次时间同步误差，因此修正后的时间误差是td - td_i。其次row_i是角点图像坐标的纵坐标，ROW图像坐标纵坐标的最大值，因此TR / ROW * row_i就是相机 rolling 到这一行时所用的时间。velocity_i是该角点在归一化平面的运动速度。所以最后得到的pts_i_td是处理时间同步误差和Rolling shutter时间后，角点在归一化平面的坐标。

先验残差项

先验残差项是所有残差项里面最复杂的一部分，但是又是不可或缺的。我们先从宏观的角度来分析这个先验残差项到底在干什么。
之前我们提到，为了限制优化变量的数目，VINS-Mono 采用了滑动窗口的形式，待估计量均为滑动窗口内的状态变量。当有新的图像帧加入到滑动窗口中，需要去除滑动窗口内一个旧的图像帧以及相关的状态量，以保证滑动窗口内的状态量数目保持稳定。VINS-Mono根据当前帧是否为关键帧，会执行两种不同的滑动窗口的策略。滑窗策略留到下一章节再讨论，但不管执行哪种滑窗策略，都会从滑动窗口中删除某个图像帧，而这个图像帧通过 IMU 预积分和观测到某些地图点，会与滑动窗口内的某些其他图像帧之间产生约束关系，如果直接把该图像帧从滑动窗口内删除，会白白丢失这些约束关系，从而降低滑动窗口内状态量的优化结果。那么怎么才能即丢掉某个图像帧，只优化滑动窗口内的状态量，又保留这个丢掉的图像帧与滑动窗口内图像帧状态量之间的约束关系呢？这个时候就要派出神器—边缘化 (Marginalization) 。先验残差项就是通过边缘化得到的。这部分的知识主要参考了贺一家大神的博客[4][5]。关于构造边缘化残差项的数学知识很多，这里我简单引用一下边缘化的结论。假设需要边缘化的变量为 $x_m$，也就是对应上面提到的滑窗过程中要被丢掉的图像帧的状态量。需要求解的变量为$x_b$，即对应滑动窗口内所有的状态量。如果不丢弃$x_m$，在求解残差 $\min\limits_{x}e=f(x)$ 的最小值时，用高斯牛顿方法将构造 $H \delta x = b$，然后用 $\delta x$ 去更新 $x$ ，得到一个更准确的状态估计。然而现在要丢弃 $x_m$，只估计 $x_b$。 因此可以把 $H \delta x = b$ 写成另外一种形式
$$
\begin{bmatrix} H_{mm} & H_{bm}^T \\ H_{bm} & H_{bb} \end{bmatrix} \begin{bmatrix} x_{m} \\ x_{b} \end{bmatrix} = \begin{bmatrix} b_{m} \\ b_{b} \end{bmatrix}
$$
通过高斯消元可以变成如下形式：
$$
\begin{bmatrix} H_{mm} & H_{bm}^T \\ 0 & H_{bb}-H_{bm}^TH_{mm}^{-1}H_{bm} \end{bmatrix} \begin{bmatrix} x_{m} \\ x_{b} \end{bmatrix} = \begin{bmatrix} b_{m} \\ b_{b}-b_{m}H_{mm}^{-1}H_{bm} \end{bmatrix}
$$

也就是说通过构造 $(H_{bb}-H_{bm}^TH_{mm}^{-1}H_{bm}) \delta x_b = b_{b}-b_{m}H_{mm}^{-1}H_{bm}$ 的方式求解 $\delta x_b$，然后更新$x_b$ ，完全可以达到即丢弃 $x_m$，又保留其与 $x_b$ 之间的约束关系。
先验残差项将被构造成 $ e_{priori} = \dfrac{1}{2}\left | \hat{x_b} - x_b \right |^2 $。因此 $\min\limits_{x}e=f(x)$ 就可以等价于 $\min\limits_{x_b} e = e_{priori} + f(x_b)$。优化变量从 $x$ 变成了 $x_b$。
接下来再着重分析一下 $H$ 矩阵。在高斯牛顿法中，$H$ 是用 雅可比矩阵 $J$ 来近似的，即 $H=J^TJ$，那么当对 $H$ 进行分解得到 $H_{mm} ,H_{bm},H_{bb}$ 对应到 $J$ 上是什么东西？其实 $J$ 本身可以拆解为两个部分，第一部分是残差对于 $x_m$ 的雅可比矩阵，用 $J_m$表示，第二部分是残差对于 $x_b$ 的雅可比矩阵，用$J_b$表示。则有 $H_{mm}= J_m^TJ_m, H_{bm}= J_b^TJ_m, H_{bb}= J_b^TJ_b$。
理论部分大致是这样的原理，但对应到 VINS-Mono 的源码中，这将是一个非常复杂的过程。
但总体上先验残差项的构造可以分为以下几个步骤：
1.把上一次先验项中的残差项传递给当前先验项，并从中去除需要丢弃的状态量
2.添加与当前需要丢弃的状态量相关的约束项
3.通过函数void MarginalizationInfo::preMarginalize()得到每个残差项对应的参数块，雅可比矩阵，残差值。
4.通过函数void MarginalizationInfo::marginalize()将步骤3中得到的雅可比矩阵和残差值进行组合，得到整个先验项的参数块，雅可比矩阵和残差值。

通过以上四步先验项就算构造完成了，在对滑动窗口内的状态量进行优化时，把它与 IMU 残差项和视觉残差项放在一起优化，从而得到不丢失历史信息的最新状态估计的结果。

滑窗策略

根据当前帧是否为关键帧，VINS-Mono 中将会采用两种不同的策略。这两种策略可以用下图解释：

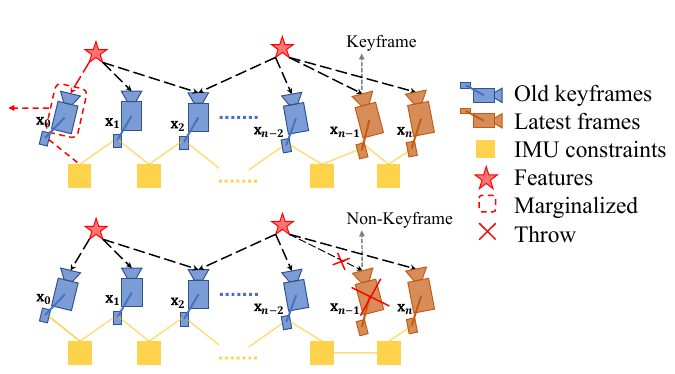
如果当前帧是关键帧，则丢弃滑动窗口内最老的图像帧，同时对与该图像帧关联的约束项进行边缘化处理。这里需要注意的是，如果该关键帧是观察到某个地图点的第一帧，则需要把该地图点的深度转移到后面的图像帧中去。
如果当前帧不是关键帧，则丢弃当前帧的前一帧。因为判定当前帧不是关键帧的条件就是当前帧与前一帧视差很小，也就是说当前帧和前一帧很相似，这种情况下直接丢弃前一帧，然后用当前帧代替前一帧。为什么这里可以不对前一帧进行边缘化，而是直接丢弃，原因就是当前帧和前一帧很相似，因此当前帧与地图点之间的约束和前一帧与地图点之间的约束是很接近的，直接丢弃并不会造成整个约束关系丢失信息。这里需要注意的是，要把当前帧和前一帧之间的 IMU 预积分转换为当前帧和前二帧之间的 IMU 预积分。

参考文献

[1] On-Manifold Preintegration for Real-Time Visual-Inertial Odometry
[2] Quaternion kinematics for the error-state Kalman filter
[3] https://www.zhihu.com/question/64381223
[4] https://blog.csdn.net/heyijia0327/article/details/53707261
[5] https://blog.csdn.net/heyijia0327/article/details/52822104