VINS-Mono中的VIO初始化

发表于 | 分类于 ， | | 阅读次数:
VINS-Mono中的 VIO 初始化相关代码学习

摘要

VIO 初始化对于 VIO 系统来讲十分重要，VINS-Mono对初始化这块比较重视，相关论文也发了不少，本篇博客将从原理出发，对相关代码进行梳理。
VINS-Mono中VIO初始化的入口为bool Estimator::initialStructure()。整个初始化过程主要有如下几个步骤。

视觉初始化

VIO 初始化的依赖于视觉的初始化。VINS-Mono的视觉初始化与一般的单目初始化差别不大。这里有几个关键的数据结构。其中一个是vector<SFMFeature> sfm_f，里面保存的是某个角点在一系列图像中归一化坐标，保存在observation变量在中。另一个是map<double, ImageFrame> all_image_frame;。还有一个是FeatureManager f_manager。FeatureManager f_manager相对有些复杂，我们来着重分析一下。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
map<double, ImageFrame> all_image_frame; // 键是时间戳，值是图像帧，图像帧中保存了图像帧的位姿，预积分量和关于角点的信息
class ImageFrame
{
	map<int, vector<pair<int, Eigen::Matrix<double, 7, 1>> > > points;
	double t;
	Matrix3d R;
	Vector3d T;
	IntegrationBase *pre_integration;
	bool is_key_frame;
};
vector<SFMFeature> sfm_f;
struct SFMFeature
{
    bool state;
    int id; // 角点的id
    vector<pair<int,Vector2d>> observation; // 保存了这个角点在一些列图像中的归一化坐标，以及那些图像帧的id。
    double position[3]; // 保存角点的三维坐标
    double depth;
};
class FeatureManager{
	...
    list<FeaturePerId> feature; // 通过FeatureManager可以得到滑动窗口内所有的角点信息
}
class FeaturePerId{
    // 以feature_id为索引，并保存了出现该角点的第一帧的id，
	...
    const int feature_id;
    int start_frame;
    vector<FeaturePerFrame> feature_per_frame;	
}
class FeaturePerFrame{
	// 保存了归一化坐标，图像坐标以及深度	
	...
    Vector3d point;
    Vector2d uv;
    double z;
}

简单地说，通过FeatureManager f_manager，我们可以查询当前滑动窗口中能够观测到的所有角点，以及这些角点被滑动窗口内的哪些帧观测到了。利用FeatureManager f_manager保存的信息，可以得到vector<SFMFeature> sfm_f，作为后续单目初始化的数据关联。
在真正进行初始化之前，会对视差进行检查，依赖的函数的是bool Estimator::relativePose(Matrix3d &relative_R, Vector3d &relative_T, int &l)。当平均视差大于30并且通过基础矩阵求解得到的内点数目大于12，可以认为当前的角点匹配足够支持单目初始化。从Estimator::relativePose中还可以得到当前帧和滑动窗口内哪一帧(保存在变量l中)是视差足够的，并计算当前帧与第l帧之间的R和T，计算得到R和T其实已经完成了一部分的初始化。

真正的完成单目初始化在bool GlobalSFM::construct(...)中，这个函数主要经历了如下几个步骤来完成初始化。
1.通过得到有足够视差的l帧和与当前帧之间的R和T进行三角化得到地图点，即调用void GlobalSFM::triangulateTwoFrames(...)。
2.有了三角化的地图点之后，对第l帧和当前帧之间所有的图像帧通过 pnp 求解其位姿，即调用bool GlobalSFM::solveFrameByPnP(...),得到位姿之后，再次进行三角化得到新的地图点。
3.利用已有的地图点，对l之前的所有图像帧进行 pnp 求解其位姿，然后再次进行三角化得到新的地图点。
4.对于其他没有被三角化的角点，再次进行三角化得到新的地图点。
5.通过一次 full BA 来对地图点和滑动窗口内的关键帧位姿进行优化。这里的 full BA 只对滑动窗口内的关键帧位姿作优化，而不优化地图点。VINS在建立重投影误差的时候很有意思，它并不在图像平面求像素误差，而是在归一化平面求误差。
6.在视觉初始化的最后，再次对所有的帧求解一次 pnp。因为前5步只得到了滑动窗口内所有关键帧的位姿，但由于并不是第一次视觉初始化就能成功，此时图像帧数目有可能会超过滑动窗口的大小(根据图像帧的视差判断是否为关键帧，然后选择滑窗的策略)，此时要对那些不被包括在滑动窗口内的图像帧位姿进行求解。

此时可以说，整个视觉初始化部分就完成了。

视觉-IMU对齐

VIO初始化的有两个很重要的目的。首先，通过 IMU 得到的观测量是具备绝对尺度的，而单目初始化的结果是不具备绝对尺度的，因此将 IMU 的观测值作为观测量加入到视觉初始化的结果中，可以恢复出视觉初始化缺失的尺度。其次，IMU的观测结果是否准确，在很大程度上依赖于对 IMU 加速素和角速度的 bias 估计是否准确，此时将视觉的观测结果作为约束项加入到 IMU 的积分计算中，可以得到 bias 的初始估计。 VINS-Mono在将视觉观测和 IMU 观测对齐时，一共经历了4个步骤。

第一步是角速度(bias) $b_w$ 的估计。
这部分的代码在void solveGyroscopeBias(map<double, ImageFrame> &all_image_frame, Vector3d* Bgs)中。
对于连续的两帧图像，通过之前的初始化得到了其在世界坐标系下的旋转 $q_{wi},q_{wi+1}$，通过 IMU 预积分得到 $\delta q_{ii+1}$，因此有
$q_{wi}^T q_{wi+1} = \Delta q_{i,i+1} \otimes \begin{bmatrix}
1\\
\frac{1}{2} J^{\delta q^{i,i+1}}_{b_{wi}} \delta b_{wi}
\end{bmatrix} $。联立所有相邻图像帧得到一系列的方程。假设在整个初始化期间角速度的 bias 是固定的，则这一系列方程只有 $\delta b_{w}$是未知的。联立的方程可以写成关于 $\delta b_{w}$ 的超定方程，通过矩阵分解的一些技巧可以得到最小二乘解。在 VINS-Mono 中采用的是通过 LDLT 分解求解$\delta b_{w}$。得到 $\delta b_{w}$ 之后，通过 $\delta b_{w}$ 重新计算所有的预积分量，即调用函数void IntegrationBase::repropagate(...)。

第二步是对每一个图像帧的速度$V_i$，重力$g$和尺度$s$进行估计。
首先解释一下两个公式。
在VIORB的论文中给出了这样一个公式: $P_{wb} = s P_{wc} + R_{wc}P_{cb} \qquad (1)$
在VINS-Mono中给出的公式是这样的：$sP_{wb} = sP_{wc} - R_{wb}P_{bc} \qquad (2)$
乍一看两个公式不一样，其实仔细分析下两个公式是等价的。两个公式的左边都是 IMU 坐标系在世界坐标系下的位姿，只是定义不一样。VIORB中$P_{wb}$是具备尺度的位姿，而在 VINS-Mono 中$P_{wb}$是不具备尺度的位姿。
而$P_{cb} = -R_{cb}P_{bc}$，因此有$ R_{wc}P_{cb} = -R_{wc}R_{cb}P_{bc} = -R_{wb}P_{bc}$。所以两个公式其实是完全等价的。

根据之前学习的 IMU 预积分理论，有如下两个预积分约束：
$$
\delta V_{i,i+1} = R_{wbi}^T ( R_{wbi+1} V_{i+1} - R_{wbi} V_{i} + g\delta t ) \qquad (3)\\
\delta P_{i,i+1} = R_{wbi}^T ( P_{wbi+1} - P_{wbi} - R_{wbi} V_{i} \delta t + \frac{1}{2} g\delta t^2 ) \qquad (4)
$$

把带有 $s$ 变量的公式(2)代入公式(4)可得：
$$
\delta P_{k,k+1} = R_{wbk}^T ( s(P_{wck+1} - P_{wck}) - (R_{wbk+1}-R_{wbk})P_{bc} - R_{wbk} V_{k} \delta t + \frac{1}{2} g\delta t^2 ) \qquad (5)
$$

联立公式(3)和公式(5)，可以得到一系列的方程。
其中$R_{wbk} = R_{wck} R_{cb}$，因此方程的未知项为$V_k，g 和 s$。在 VINS-Mono 将其写成矩阵形式，其中 $XI$ 表示未知项。通过矩阵分解的方法求解 $H_{b_{k+1}}^{b^{k}} X_I = z_{b_{k+1}}^{b^{k}}$。



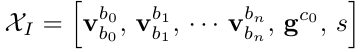
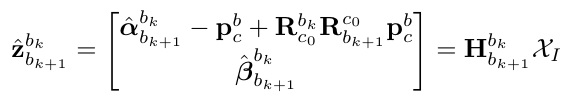
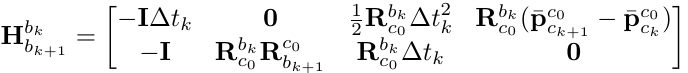
第三步是对重力 $g$ 进行修正。

由于第二步中求解的 $g$ 在一定程度上是有误差的。而一般来说，重力大小(magnitude)是已知，因此可以根据这个先验，对 $g$ 进行进一步的修正。
假设重力大小为G，则有 $g = G \cdot \hat{g} + w_1b_1 + w_2b_2$，其中 $\hat{g}$ 是我们在第三步中求解得到 $g$ 的方向(单位向量)，$b_1$, $b_2$ 在 $\hat{g}$ 的正切平面上，并且正交。也就是说$b_1,b_2,\hat{g}$ 构成标准正交基。$b_1,b_2$ 的设置如下图所示

把 $g = G \cdot \hat{g} + w_1b_1 + w_2b_2$ 代入到公式(2)和公式(4)中，此时不再求解 $g$，而$b_1,b_2$是已知的，因此只需要求解$w_1,w_2$。即$X_I = [V_0,…,V_n,w_1,w_2,s]$。也就是说对重力 $g$ 进行修正的同时，也会对 $V_i$ 和 $s$ 进行调整。
此时 $z_{b_{k+1}}^{b_k}$ 的第一项要减去 $\frac{1}{2} R_{c_0}^{b_k} G \cdot \hat{g} \delta t^2$，第二项要减去 $R_{c_0}^{b_k} G \cdot \hat{g} \delta t$，其他的和第二步保持一致。
这部分的代码在void RefineGravity(...)。为了使得 g 的值可以收敛，void RefineGravity(...)中对 $H_{b_{k+1}}^{b^{k}} X_I = z_{b_{k+1}}^{b^{k}}$ 方程迭代求解4次。

其实对这一步修正 g 的原理有一点迷。第二步求解的 $g$ 的大小(magnitude)与实际的重力大小不一致，除了有噪声的影响外，加速度计的 bias 的影响应该也是存在的。这里的修正感觉上是通过找出修正重力方向的 $w_1b_1$ 和 $w_2b_2$。$G \cdot \hat{g}$ 强行将 $g$ 的大小拉扯到实际的重力大小，然后另 $g = G \cdot \hat{g} + w_1b_1 + w_2b_2$，也就是说用 $w_1b_1+w_2b_2$ 代替噪声和加速度计的 bias 对 $g$ 的影响。求解出 $w_1,w_2$ 之后，最后得到的重力的方向为 $g = G \cdot \hat{g} + w_1b_1 + w_2b_2$ 的单位方向向量。很迷很迷…

第四步完成初始化
得到重力 $g$ 之后，即可根据其与方向向量[0,0,1]之间的旋转，得到世界坐标系与第一帧相机坐标系之间旋转，从而可以将所有图像帧的旋转转换到世界坐标系下。其次根据得到的尺度$s$，对地图点坐标和平移进行缩放。这部分代码在void visualInitialAlign()函数的后半部分。

总结

谜一样的重力修正求解答。> - <