摘要
考完雅思,写完硕士论文,各种乱七八糟的事在瞎忙,总算有时间好好看看文章了。
IMU预积分在IMU与单目视觉SLAM融合中起到了非常关键的作用,很多VIO系统都是基于IMU预积分理论进行实现的。这篇论文算上附录总共85个公式,又一次让我感慨,数学是由多重要。
借助IMU,可以有效地解决单目SLAM系统尺度不确定问题和尺度漂移问题,极大地提升了单目SLAM系统的实用性。
在很多公式看不大懂的前提下,本文将基于论文严密的数学推导,用简单的思想进行概括,希望能够理清楚思路。
ps:公式编号遵循论文。
状态估计
所有的SLAM问题都可以建模成状态估计问题,通过相机或者激光的约束方程,来对需要估计的状态进行约束,从而得到状态估计的最优估计。在VIO中,可以建立如下的状态估计问题:
$$ x_i \doteq [R_i, p_i, v_i, b_i] \quad (22)$$
其中下标$i$表示某个时刻,$(R_i, p_i)$表示机器人的位姿,即旋转矩阵和平移向量。$v_i \in \mathbb{R^3} $表示速度。$b_i=[b_i^g, b_i^a] \in \mathbb{R^6}$表示IMU中加速度计和陀螺仪的偏差。$X_k \doteq \{x_i\}_{i\in K_k}$都是在系统运行过程中未知的,需要我们通过观测数据来进行估计的。
OK,那我们有哪些观测数据呢?当然就是相机数据和IMU数据了。用如下变量表示:
$$ Z_k \doteq \{C_i, I_{ij}\}_{(i,j) \in K_k} $$
其中$C_i$表示图像关键帧,$I_{ij}$表示两个连续关键帧之间的IMU数据。
因此整个状态估计问题就可以建模成基于观测数据$Z_k$,求$X_k$的最大后验
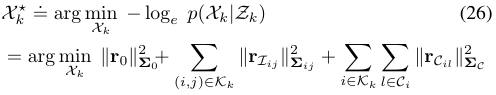
其中$r_{I_{i,j}}$是基于IMU数据的残差值,$r_{C_{i,l}}$是基于图像数据的残差值。因此,要求解这个状态估计问题,理清楚$r_{I_{i,j}}$和$r_{C_{i,l}}$的表达方式非常重要。
IMU模型
IMU数据包含两个部分,三轴加速度数据和三轴角速度数据。我们观测得到的加速度数据和角速度数据与实际值之间还相差了一个偏差$b$和噪声$\eta$。如下图所示: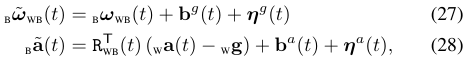
其中坐标为观测到的IMU数据,这些数据包含了噪声和偏差。B表示为IMU坐标系,W表示为世界坐标系。世界坐标系下,IMU的位姿用$ \{ \mathrm{R_{WB}}, \mathrm{_Wp} \}$ 表示。 $\mathrm{_w g}$表示世界坐标系下的重力向量。
从加速度推算速度和位移,以及从角速度推算旋转有如下的积分关系:
由于从IMU中获取的数据是离散的,因此需要将积分形式转为差分形式: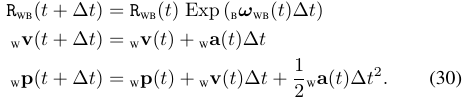
式(30)中的$\mathrm{_wa(t)}$和$\mathrm{_w \omega_{WB}(t)}$均为理论值,与实际的观测值之间相差一个偏差和噪声,用式(27)和式(28)对式(30)进行替换,得到:
IMU误差项
式(31)从理论上是可以作为$r_{I_{i,j}}$的约束条件的,但是由于IMU获取观测数据的频率非常高,这会导致约束条件过多,从计算速度上来说是不可行的。预积分就是要解决这个问题。基本思路就是将两个关键帧(i和j)之间的所有IMU数据进行一个计算,使其称为关键帧i和关键帧j的一个运动约束。如下图:
但是式(32)存在一个致命的问题,就是当$t_i$时刻的状态(如$R_{i}$)发生变化时,所有的运动约束关系都需要重新计算,因此引入一个增量的概念,使得$i$时刻和$j$时刻之间的约束关系只与IMU的观测数据有关,而与当前的状态无关,如下图所示: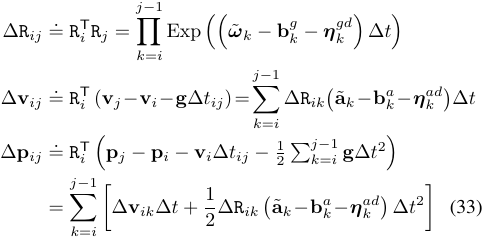
式(33)是预积分中的关键,它可以直接利用IMU的观测数据计算得到,作为$r_{I_{i,j}}$的约束条件。后续所有的公式都是围绕怎么计算这个公式,以及如何在非线性优化中计算状态估计的更新量。
式(33)应该包含了一次坐标转换,将世界坐标系下的物理量转换到了i时刻IMU的坐标系下的物理量。(待商榷)
式(33)已经建立了关键帧之间的系统状态与IMU数据之间的关联关系。利用式(33)构造式(26)的IMU残差项时,还会存在一个会头疼的问题,协方差矩阵怎么搞?
为了求这个协方差矩阵,又要开始堆公式了…
首先是将噪声数据从观测数据中分离出来: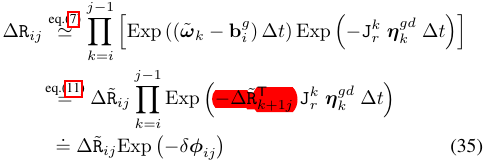
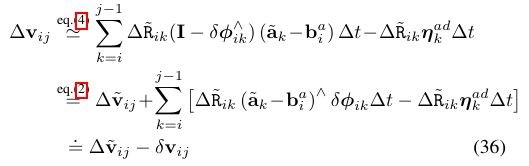
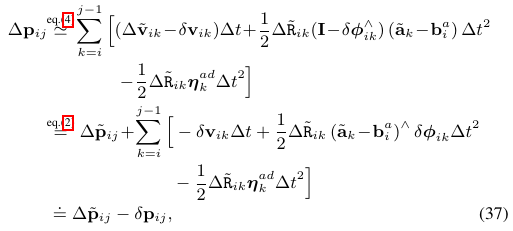
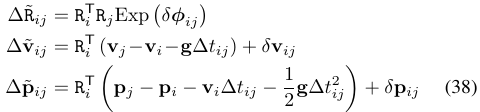
主要利用的是右乘BCH近似雅可比和对数映射的一些运算公式。
公式(38)想要表达的意思就是通过观测值得到预积分,跟通过实际值得到的预积分,就是相差一个误差项而已,通过分析这个误差项,我们就可以得到关于IMU误差项的协方差矩阵。又要开始作者的表演。
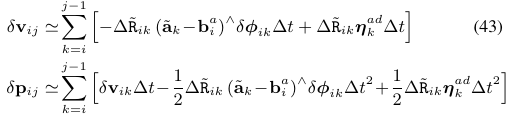
总算证明出误差项在一阶近似的情况下,是对每一时刻的高斯噪声的线性组合,因此还是高斯噪声。这下可以通过一种线性传播的方式来求解每一个IMU预积分项的协方差矩阵了。在论文的附录A中给出了协方差矩阵的迭代求解方式。
讲完了误差项,再讲一讲偏差项。在上述的所有推导中,我们都是假设偏差项$b_i$是不变的,但在实际中,$b_i$是会随时间变化的一些列数值,通常可以认为是一种布朗运动。因此当我们在优化IMU残差项的过程中,会执行$b_i=\bar{b} + \delta b$更新,如果每得到一个新的$b_i$就重新计算一次预积分,计算量是不可接受的。因此利用一阶展开,可以对预积分进行增量更新。
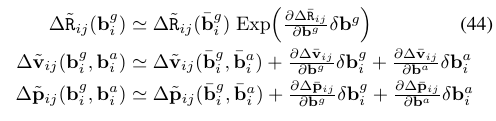
公式中出现N多的雅可比都是可以在预积分过程中预先计算的。公式(44)的证明以及雅可比的计算方式在论文的附录B中给出了。
有了上面这么多的公式,总算可以构造我们的IMU误差项了:
在对误差项利用高斯牛顿法求解时,需要求解待优化变量的雅可比矩阵,其求解方式在论文附录C中给出。
另外,为了使得IMU的偏差符合布朗运动,另外添加一项约束到IMU误差项中: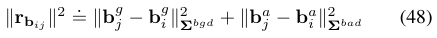
视觉误差项
回顾一下式(26)中的视觉残差项:
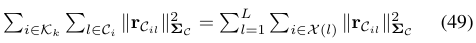
一个标准的视觉残差模型如下所示:
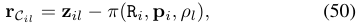
式(50)中如果对所有的地图点$\rho_l$进行优化,会带来不小的计算开销,因此论文采用了一种structureless approach的方法,来避免对地图点进行优化。
在高斯牛顿法的迭代过程中,将求解如下的最小二乘问题,从而得到系统状态估计的更新量$\delta \phi _i, \delta p _i, \delta \rho _l$。

式(51)中$\check{\pi}(\cdot)$使用了一次李代数上的扰动模型。
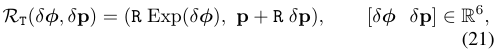
求解式(51)的常用办法就是作线性展开,得到:
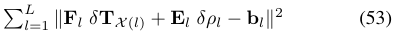
其中若将$\delta T _{x(l)}$作为已知项,求式(53)的最小二乘则有:
将式(54)代入式(53),整个求解问题就转变为了: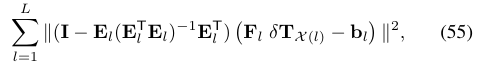
论文这一部分的动机是将地图点从整个优化问题中去除出去,运用了一种Schur complement trick的BA方法,但是为什么不像ORB-SLAM那样固定地图点,而只优化位姿呢?这部分内容还需要结合相关材料在深入理解。
参考文献
1.On-Manifold Preintegration for Real-Time Visual-Inertial Odometry