摘要
之前提到三维空间中的运动可以用旋转矩阵和变换矩阵来描述,旋转矩阵是一种特殊正交群SO(3),而变换矩阵是特殊欧式群SE(3)。但是群到底是个什么玩意?这篇博客将会作简单介绍。
李群
群(Group)是一种集合加上一种运算的代数结构。把集合记作$A$,运算记做$\cdot$,那么群可以记做$G=(A,\cdot)$。群要求这个运算满足以下几个条件:
1.封闭性:$\forall a_1,a_2 \in A,\ \ a_1 \cdot a_2 \in A$
2.结合律:$\forall a_1,a_2,a_3 \in A, \ \ (a_1 \cdot a_2)\cdot a_3 = a_1 \cdot (a_2 \cdot a_3)$
3.幺元:$\exists a_0 \in A, \ s.t. \ \forall a \in A, \ a_0 \cdot a = a \cdot a_0 = a$
4.逆:$\forall a \in A, \ \exists a^{-1} \in A \ \ s.t. \ \ a \cdot a^{-1}=a_0$
可以验证旋转矩阵和矩阵乘法构成群,变换矩阵和矩阵乘法也构成群。
李群是指具有连续(光滑)性质的群。$SO(3)$和$SE(3)$在实数空间上是连续的,因此都是李群。
李代数
考虑旋转矩阵$R$是正交矩阵,因此有:
$RR^T=I$
不妨设$R$会随时间变化,即为时间的函数$R(t)$,此时有:
$R(t)R(t)^T=I$
对等式两边求导有:
$\dot{R}(t)R(t)^T+R(t)\dot{R}(t)^T=0$
$\dot{R}(t)R(t)^T=-(\dot{R}(t)R(t)^T)^T$
因此$\dot{R}(t)R(t)^T$是一个反对称矩阵,记对应的三维向量为$\phi(t)$,则$[\phi(t)]_{\times}=\dot{R}(t)R(t)^T$
此时有:
$\dot{R}(t)=[\phi(t)]_{\times}R(t)$
也就是说对于每个旋转矩阵,存在一个反对称矩阵,两者的乘积即为这个旋转矩阵的导数。其实这个反对称矩阵对应的三维向量就是李代数。每个李群都有与之对应的李代数。李代数描述了李群的局部性质。
旋转矩阵$SO(3)$对应的李代数为$\mathfrak{so}(3)$。
变换矩阵$SE(3)$对应的李代数为$\mathfrak{se}(3)$。值得注意的是$\mathfrak{se}(3)$位于一个六维空间中。假设$\mathfrak{se}(3)$的元素为$\xi$,则有:
$\mathfrak{se}(3)=\{ \xi=\begin{bmatrix}
\rho \\
\phi
\end{bmatrix} \in \mathbb{R}^6,\rho \in \mathbb{R}^3, \phi \in \mathfrak{so}(3), [\xi]_{\times} = \begin{bmatrix}
[\phi]_{\times} & \rho \\
0^T & 0
\end{bmatrix} \in \mathbb{R}^{4 \times 4} \}$
$\xi$ 的前三维与变换矩阵中的平移向量相关,后三维则与旋转向量相关(其实就是旋转向量),而$[\xi]_{\times}$不再严格代表反对称矩阵。
李代数的数学定义不展开详述了。
指数与对数映射
通过求解$R$关于 $\phi$ 的微分方程我们可以得到两者之间存在指数关系,即:
$R=\mathbf{exp}([\phi]_{\times})$
但是矩阵作为指数是个什么鬼,要怎么算?在李群和李代数中,称为指数映射。
由于$\phi$是三维向量,可以定义$\phi=\theta a$。其中$\theta$表示方向,$a$表示大小。
用泰勒展开式可得:
$
\begin{equation}
\begin{aligned}
R = \mathbf{exp}([\phi]_{\times}) &= \mathbf{exp}(\theta [a]_{\times}) = \sum^{\infty }_{n=0} \dfrac{1}{n!}(\theta [a]_{\times})^n \\
&= … \\
&= \cos \theta I + (1-\cos\theta)aa^T + \sin \theta [a]_{\times}
\end{aligned}
\end{equation}
$
这个公式与我们在三维空间中的刚体运动里提到的旋转矩阵和旋转向量之间的转换一模一样。也就是说此处的指数映射就是罗德里格斯公式。至此我们得到了$\mathfrak{so}(3)$到$SO(3)$的转换。
那么如何从$SO(3)$中得到对应的$\mathfrak{so}(3)$呢?这就是李群和李代数中的对数映射。
在之前我们已经介绍过如何用旋转矩阵来求解旋转向量,此处的求解方式也是相同的。即:
$\theta = \arccos(\dfrac{tr(R)-1}{2})$
由于旋转轴上的向量在旋转后不发生改变,说明:
$Rn = n$
因此转轴$n$是矩阵$R$特征值1对应的特征向量。求解此方程,再归一化,就得到了旋转轴。
需要注意的是从$R$中求解 $\phi$ 并非是一一对应的。从一个$R$中可以求解多个相应的$\phi$。从几何的角度来理解,旋转是具有周期性的,因此会存在多个$\phi$。
说了$SO(3)$,我们再说说$SE(3)$。$SE(3)$和$\mathfrak{se}(3)$之间同样存在指数映射和对数映射。
指数映射形式如下:
$
T = \mathbf{exp}([\xi]_{\times}) = \begin{bmatrix}
R & J\rho\\
0^T & 1
\end{bmatrix}
$
其中$J=\dfrac{\sin \theta}{\theta} I + (1- \dfrac{\sin \theta}{\theta})aa^T + \dfrac{1-\cos \theta}{\theta}[a]_{\times}$
从$SE(3)$到$\mathfrak{se}(3)$的求解往往不会直接使用对数映射,而是转换到对于的$\mathfrak{so}(3)$上。对于$\rho$的求解可以构造$t=J\rho$的方程。
至此旋转矩阵和变换矩阵与对应的李代数之间的转换方式就讲完了。至于李代数到底有什么用我们留到下一篇再讲。
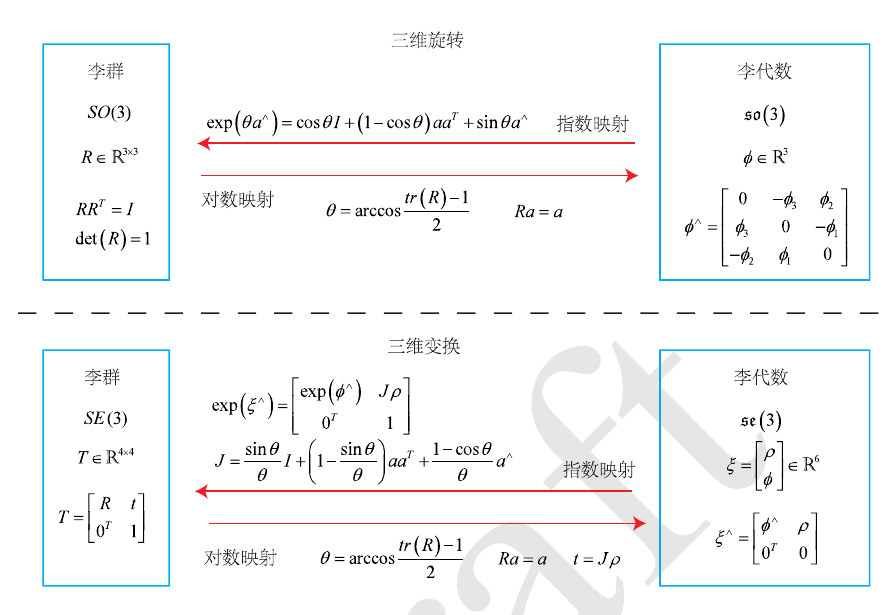
总结起来就是下图。
参考文献
1.《视觉SLAM十四讲》第四讲