摘要
之前提到通过对极几何的方式来求解相机的运动估计,即2D-2D的运动估计。但是通过对极几何来对相机进行运动估计会面临几个问题。
1.存在初始化的问题
2.不能求解纯旋转
3.尺度不一致问题
因此当已知特征点在空间中的三维坐标以和图像对应的像素坐标,我们不再使用对极几何的方式进行相机的运动估计,而采用3D-2D的方式进行运动估计。这种求解方法称为PnP(Perspective-n-Point)。
对于单目相机,特征点的三维坐标的求解需要先通过对极几何初始化,然后通过三角化测量求得。
对于双目或RGB-D相机,深度信息直接可得,因此可以直接使用PnP进行。
3D-2D方法不需要使用对极约束,最少可以用三个匹配点获得运动估计,因此是一种非常重要的相机运动估计方式。
PnP有很多种求解方式,例如用三对点进行估计的P3P,直接线性变换(DLT),EPnP,UPnP等。此外还有非线性优化的方式,构建最小二乘问题并迭代求解,也就是常用的Bundle Adjustment。
在SLAM问题中,通常的做法是先使用P3P或者EPnP等方法估计相机位姿,然后构建最小二乘优化问题对估计值进行调整(Bundle Adjustment)。因此我们将从这两个方面出发来完成3D-2D运动估计。
在2D-2D的运动估计中,我们通过两幅图像中的特征点像素坐标,通过计算得到了运动估计。
在3D-2D的运动估计中,我们将利用空间点的三维坐标和图像中的特征点像素坐标,来进行运动估计。
P3P
P3P仅需要使用三对匹配点,就可以完成相机的位姿估计。
先从几何的角度出发,假设空间中有$A,B,C$三点,投影到成像平面中有$a,b,c$三点,在PnP问题中,$A,B,C$在世界坐标系下的坐标是已知的,但是在相机坐标系下的坐标是位置的。$a,b,c$的坐标是已知的。PnP的目的就是要求解$A,B,C$在相机坐标下的坐标值。如下图所示。需要注意的是三角形$abc$和三角形$ABC$不一定是平行的。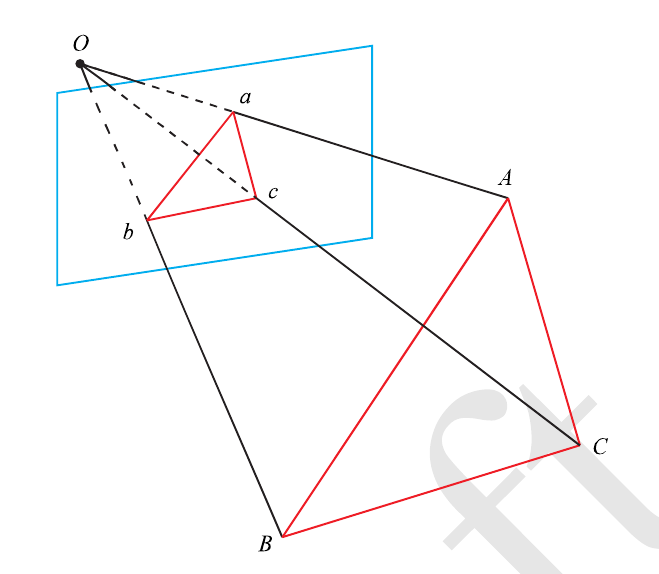
根据余弦定理有:
$
OA^2 + OB^2 - 2OA \cdot OB \cdot \cos(a,b) = AB^2 \\
OB^2 + OC^2 - 2OB \cdot OC \cdot \cos(b,c) = BC^2 \\
OA^2 + OC^2 - 2OA \cdot OC \cdot \cos(a,c) = AC^2
$
记$x=\dfrac{OA}{OC}$,$y=\dfrac{OB}{OC}$,因为$A,B,C$在相机坐标系中的坐标未知,因此$x$,$y$是未知的。
另记$u=\dfrac{BC^2}{AB^2}$,$w=\dfrac{AC}{AB}$,根据$A,B,C$的世界坐标,$u,w$是可以求出的。
通过一系列的转化可以得到两个等式:
$(1-u)y^2-ux^2-\cos(b,c)y+2uxy \cos(a,b) +1 = 0 \\
(1-w)x^2-wy^2-\cos(a,c)x+2wxy \cos(a,b) +1 = 0$
该方程组是关于x,y的一个二元二次方程,可以通过吴消元法求解。最多可能得到四个解,因此在三个点之外还需要一组匹配点进行验证。
至此,通过x和y就可以求得A,B,C在相机坐标下的坐标值。因此3D-2D问题转变成了3D-3D的位姿估计问题。而带有匹配信息的3D-3D位姿求解非常容易。
关于3D-3D的位姿估计,我们留到下一篇讲。
P3P只利用三组匹配点的信息,加一组匹配点用于验证。当给定的匹配点很多时,难以利用更多的信息。而且如果匹配点噪声明显或者匹配错误,P3P算法会失败。因此大牛们在此基础上又提出了EPnP、UPnP等方法。等有时间再谈一谈这些解法的思路。
Bundle Adjustment
假设某空间点坐标为$P_i = [X_i, Y_i, Z_i]$,其投影的像素坐标为$p_i=[u_i,v_i]$。这些在PnP问题里都是已知的。在相机坐标系下有$c=[x_i, y_i, z_i]$,这个坐标通过P3P或者其他解法有了粗略的估计。根据针孔相机模型可得:
$z_i p_i = KTP_i = K \exp([\xi]_{\times})P_i$
根据这个等式可以构造出一个最小二乘问题:
$ \xi^* = \arg \min \limits _{\xi} \dfrac{1}{2} \sum\limits _{i=1} ^n \begin{Vmatrix}
p_i - \dfrac{1}{z_i} K \exp([\xi]_{\times})P_i
\end{Vmatrix} _2 ^2$
该问题的误差项,是将像素坐标与3D点按照当前估计的位姿进行投影得到的位置相比较得到的误差,所以称之为重投影误差。如图下图所示。
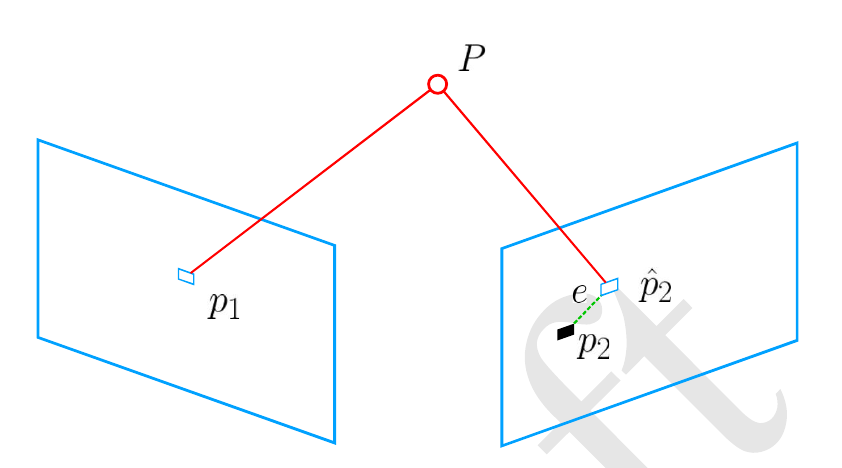
这个最小二乘问题主要优化两个变量,第一是对相机位姿的优化,也就是对李代数的优化,第二是对空间点$P$的优化,也就是P点的优化。因此涉及到了两个关键的求导问题。
关于李代数的求导,涉及到之前介绍的扰动模型进行,此处直接给出求导结果:
$\dfrac{\partial e}{\partial \Delta\xi} = -\begin{bmatrix}
\frac{f_x}{z} & 0 & - \frac{f_x x}{z^2} & -\frac{f_xxy}{z^2} & f_x+\frac{f_xx^2}{z^2} & -\frac{f_xy}{z} \\
0 & \frac{f_y}{z} & -\frac{f_y y}{z^2} & -f_y-\frac{f_yy^2}{z^2} & \frac{f_y xy}{z^2} & \frac{f_y x}{z}
\end{bmatrix}$
关于位姿的求导,有:
$\dfrac{\partial e}{\partial \Delta\xi} = -\begin{bmatrix}
\frac{f_x}{z} & 0 & - \frac{f_x x}{z^2} \\
0 & \frac{f_y}{z} & -\frac{f_y y}{z^2}
\end{bmatrix}R$
参考文献
- 《视觉SLAM十四讲》第七讲