摘要

利用两幅图像以及匹配的特征点，我们已经能够利用对极几何估计相机的运动，即得到旋转矩阵$R$和平移向量$t$。但是如何进一步得到特征点在三维空间中的位置？这就涉及到三角化测量的方法。

三角化测量

假设P是三维空间中的某一点，在两幅图像中的像素坐标分别为$p_1$和$p_2$，在相机坐标系下的坐标为$c_{1}$和$c_{2}$，根据针孔相机中的坐标变换公式可知：
$z_{1}p_1=Kc_{1}$
$z_{2}p_2=Kc_{2}$
其中$z_{1}$是$c_{1}$在$Z$轴上的坐标，$z_{2}$是$c_{2}$在$Z$轴上的坐标，$K$是相机的内参矩阵。

不妨令：
$p_1=Kx_{1}$
$p_2=Kx_{2}$
其中$x_{1},x_{2}$称为点P在相机坐标系下的归一化坐标。

根据三维空间中的运动模型有：
$c_2 = Rc_1 + t \\
k^{-1}z_1p_1 = R k^{-1}z_2p_2 + t \\
z_1 x_1 = z_2 R x_2 + t$

同时左乘$x_1$的反对称矩阵可得：

$z_1 [x_1]_{\times} x_1 = 0 = z_2 [x_1]_{\times}Rx_2 + [x_1]_{\times}t$

上述等式的右边是个关于未知变量$z_2$的方程，求解此方程即可得到$z_2$。有了$z_2$，$z_1$也就迎刄而解了。

但由于误差的存在，上述方程通常不会严格成立，所以更常见的做法是求最小二乘解而不是零解。

三角测量的矛盾

三角化测量的前提是两幅图像之间存在平移。有平移才会由对极几何中的三角形，才谈得上三角化测量。
如下图所示，当平移很小时，深度估计的不确定性会增大。因此要使深度的精确度增加，则需要增加平移，但是增加平移会导致图像的外观发生明显的变化，使得特征提取和匹配的难度增加，这称为三角测量的矛盾。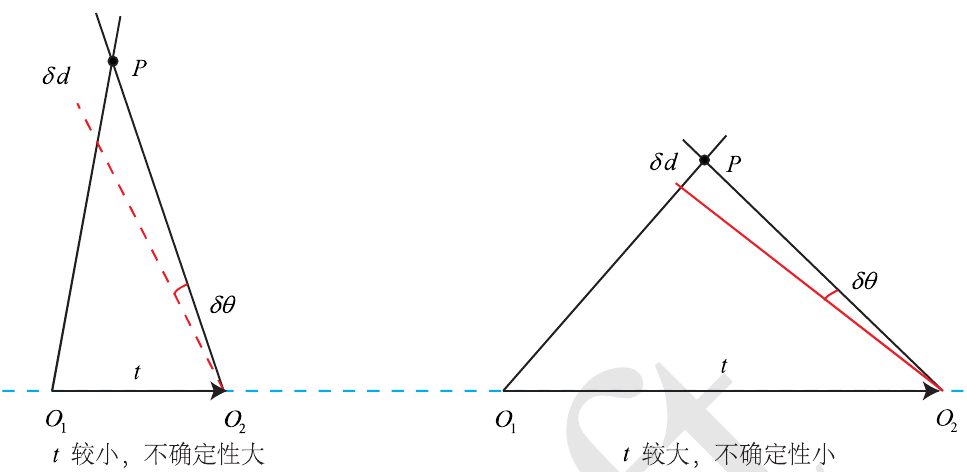

参考文献

1.《视觉SLAM十四讲》第七讲