图片全部来源互联网,如有侵权,跟我说一声。
摘要
这篇博客是关于学习针孔相机模型过程中的一些简单记录。
坐标系
相机模型中常常涉及到四个坐标系:图像像素坐标系,成像平面坐标系,相机坐标系和世界坐标系。人类真是复杂…
图像像素坐标系
图像像素坐标系通常简称为图像坐标系或者像素坐标系。如下图所示。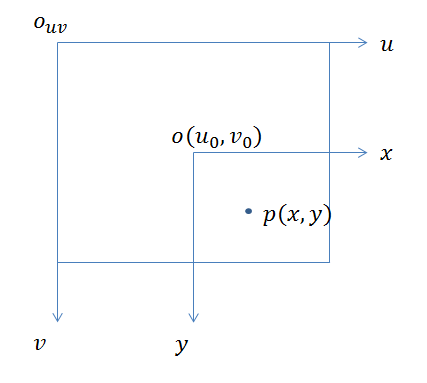
像素坐标系的平面为相机的成像平面,原点在图像的左上方,u轴向右,v轴向下,像素坐标系的单位是像素(pixel),也就是我们常说的分辨率。假设某个像素点p坐标为$(u,v)$
成像平面坐标系
成像平面坐标系和像素坐标系在同一个平面上,原点是相机光轴与成像平面的交点,通常情况下是成像平面的中点或者叫principal point。单位为物理单位,比如毫米。因此成像平面坐标系和像素坐标系只是原点和度量单位不同,两个坐标系之间相差了一个缩放比例和一个原点的平移。
假设p对应的成像平面坐标为$(x,y)$,$dx$和$dy$表示图像中每个像素在成像平面中的物理尺寸,即上面提到的缩放比例。成像平面的原点在像素坐标系中的坐标为$(u_0, v_0)$,则像素坐标系与成像平面坐标系之间有如下转换公式:
$\left\{\begin{matrix}
u= \dfrac{x}{dx}+u_{0}
\\
v= \dfrac{y}{dy}+v_{0}
\end{matrix}\right.\Rightarrow \begin{bmatrix}
u
\\
v
\\
1
\end{bmatrix} =\begin{bmatrix}
\frac{1}{dx} & 0 & u_0 \\
0 & \frac{1}{dy} & v_0 \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
x
\\
y
\\
1
\end{bmatrix}
$
相机坐标系
相机坐标系如下图所示。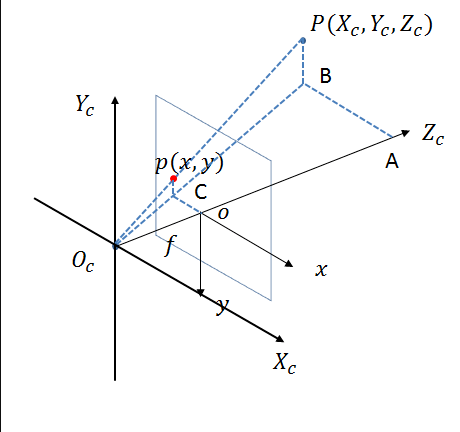
相机坐标系的原点是光心,$x_c$和$y_c$轴与像素坐标系$u$轴和$v$轴平行,$z_c$轴为相机的光轴。光心到像素平面的距离为焦距f。
由图可以看出相机坐标系上的点和成像平面坐标系上的点存在透视投影关系。假设p对应的相机坐标系下的点P的坐标为$(X_c,Y_c,Z_c)$,则成像平面坐标系与相机坐标系之间有如下转换关系:
$\left\{\begin{matrix}
x= f\dfrac{X_c}{Z_c}
\\
y= f\dfrac{Y_c}{Z_c}
\end{matrix}\right.\Rightarrow Z_c\begin{bmatrix}
x
\\
y
\\
1
\end{bmatrix} =\begin{bmatrix}
f & 0 & 0 & 0 \\
0 & f & 0 & 0 \\
0 & 0 & 1 & 0
\end{bmatrix} \begin{bmatrix}
X_c
\\
Y_c
\\
Z_c
\\
1
\end{bmatrix}
$
世界坐标系
在环境中选择一个参考坐标系来描述相机和物体的位置,该坐标系称为世界坐标系。相机坐标系和世界坐标系之间的关系可以用旋转矩阵$R$和平移向量$t$来描述。假设$P$在世界坐标系下的坐标为$(X_w, Y_w, Z_w)$,则相机坐标系与世界坐标系之间有如下转换关系:
$
\begin{bmatrix}
X_c
\\
Y_c
\\
Z_c
\\
1
\end{bmatrix} =\begin{bmatrix}
R & t \\
0 & 1
\end{bmatrix} \begin{bmatrix}
X_w
\\
Y_w
\\
Z_w
\\
1
\end{bmatrix}
$
坐标系转换
通过上述的四个坐标系可以实现从世界坐标系与像素坐标系之间的转换,如下所示:
$Z_c\begin{bmatrix}
u
\\
v
\\
1
\end{bmatrix} = \begin{bmatrix}
\frac{1}{dx} & 0 & u_0 \\
0 & \frac{1}{dy} & v_0 \\
0 & 0 & 1
\end{bmatrix} \begin{bmatrix}
f & 0 & 0 & 0 \\
0 & f & 0 & 0 \\
0 & 0 & 1 & 0
\end{bmatrix} \begin{bmatrix}
R & t \\
0 & 1
\end{bmatrix} \begin{bmatrix}
X_w
\\
Y_w
\\
Z_w
\\
1
\end{bmatrix} = \begin{bmatrix}
f_x & 0 & u_0 & 0 \\
0 & f_y & v_0 & 0 \\
0 & 0 & 1 & 0
\end{bmatrix} \begin{bmatrix}
R & t \\
0 & 1
\end{bmatrix} \begin{bmatrix}
X_w
\\
Y_w
\\
Z_w
\\
1
\end{bmatrix}
$
其中$\begin{bmatrix}
f_x & 0 & u_0 & 0 \\
0 & f_y & v_0 & 0 \\
0 & 0 & 1 & 0
\end{bmatrix}$称为内参数矩阵$K$,$\begin{bmatrix}
R & t \\
0 & 1
\end{bmatrix}$称为外参数矩阵$T$。
对于相机的内参数矩阵往往是已知的并且是固定的,而外参数矩阵在SLAM问题中往往是需要求解的,用于相机的位姿定位。
从世界坐标系到像素坐标系之间的转换关系可知,已知世界坐标系下的三维点坐标,只要已知内外参矩阵,就可以求得像素坐标。而如果已知像素坐标,即使已知内外参矩阵,其世界坐标下的三维点也不是唯一确定的,而是空间的一条直线。即单目相机只能测平面信息,而不能获取深度信息。
参考文献
- 《视觉SLAM十四讲》第五讲
- 相机成像原理:世界坐标系、相机坐标系、图像坐标系、像素坐标系之间的转换