摘要

对机器人的控制动作(motion)进行建模是计算状态转移概率$p(x_t \mid u_t, x_{t-1})$的重要组成部分。以下的所有动作模型都是基于一个机器人在一个平面上移动的场景下展开的。

预备知识

由于限定了机器人在一个平面上移动，因此可以用坐标和方向组成的向量来表示机器人的状态。即$(x, y, \theta)$。通常也称为机器人的位姿。状态转移概率$p(x_t \mid u_t, x_{t-1})$中，$x_t$表示t时刻机器人的位姿，$x_{t-1}$表示t-1时刻机器人的位姿。而$u_t$即为t时刻机器人的控制动作，在此场景下即为机器人从一个位姿转换到另一个位姿。因此对机器人的控制动作建模是计算状态转移概率的关键。
一般对机器人控制动作建模有两种方法：
1.工业机器人通常可以通过发送一个速度指令来对机器人进行控制，第一种控制动作建模方式就是利用这个速度指令来进行控制动作建模
2.通常机器人会提供里程计信息，包括运动的距离和转动的角度。第二种控制动作建模方式就是利用里程计信息来进行控制动作建模

通常来说里程计模型要比速度模型更准确，因为里程计信息是机器人运动之后通过编码器得到的，而速度是在机器人运动之前下达的。因此速度模型通常用来进行动作规划(motion planning)。而里程计模型通常用来做状态评估。

速度动作模型

在速度动作模型中，用向量$(v_t, \omega_t)$来表示动作$u_t$,其中$v_t$表示t时刻机器人的速度，$\omega_t$表示t时刻机器人的转速。

速度动作模型的闭合解算法如下图：

它的输入是t-1时刻的位姿$x_{t-1}$，t时刻的动作$u_t$，以及t时刻的假设位姿$x_t$。输出假设位姿$x_t$的概率。$\alpha_1…\alpha_6$是与机器人相关的动作误差系数。

$\mathbf{prob(x,b)}$函数计算x在0均值b方差下的概率值。计算方式通常有以下两种方法：

根据粒子滤波，也可以通过从状态转移概率中采样得到当前时刻的位姿$x_t$，采样是基于$x_{t-1}$和$u_t$进行的。基于采样的速度动作模型算法如下图：

算法的输入是$x_{t-1}$和$u_t$,输出$x_t$。$\mathbf {sample}$函数是对控制数据增加噪声扰动。

$\mathbf {sample}$函数通常有以下两种计算方法：

以上两种速度动作模型均有严格的数学推导，详见书籍5.3.3小节。

里程计动作模型

在里程计模型中，用向量$(\bar x_{t-1}, \bar x_t)$来表示$u_t$,上划线表示该位姿是通过里程计得到的，是基于机器人内部坐标的，并非全局坐标系中的位姿。通过这两个位姿信息可以得到初始旋转角度，平移和最终旋转角度。如图所示：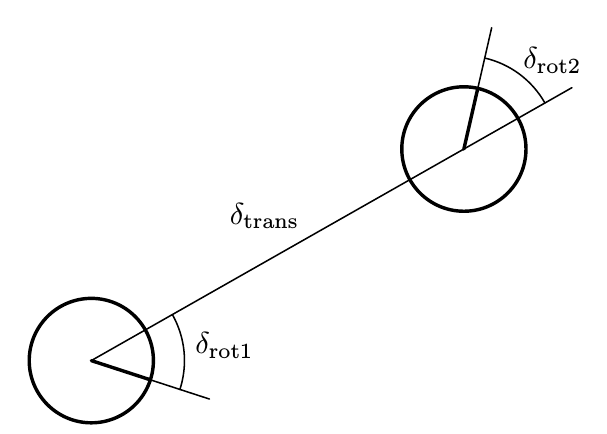

里程计动作模型的闭合解算法如下图：

它的输入是t-1时刻的位姿$x_{t-1}$，t时刻的动作$u_t$，以及t时刻的假设位姿$x_t$。输出假设位姿$x_t$的概率。$\alpha_1…\alpha_4$是与机器人相关的动作误差系数。

基于采样的里程计动作模型算法如下图：

与基于采样的速度动作模型算法基本类似，区别仅在于动作$u_t$的表示方式不同。

以上两种里程计动作模型均有严格的数学推导，详见书籍5.4.3小节。

动作与地图

以上的动作模型均未考虑机器人所在空间的地图信息。机器人在移动时是与所处空间相关的，比如某些位置已经被占用了，机器人就无法移动到这些位置上。因此需要将地图信息融入到状态转移概率中去。此时状态转移概率为$p(x_t \mid u_t, x_{t-1}, m)$。

当$x_{t-1}$与$x_t$距离足够小时(通常认为小于机器人的半径),可以用以下公式近似：
$p(x_t \mid u_t, x_{t-1}, m) = \eta \ p(x_t \mid u_t, x_{t-1}) \ p(x_t \mid m)$

融入地图信息的动作模型如图所示：

在占用地图(occupancy maps)中，如果位置已经被占用，$p(x_t \mid m)=0$

总结

本章给出了两种基本的动作模型：速度动作模型和里程计动作模型。每种模型均有闭合解版本和采样版本。这些动作模型都是基于机器人在一个平面移动的场景下的。而在实际应用中，机器人的状态可能会更加复杂，动作也更加复杂，因此不同的场景下往往会有不同的动作模型。但是原理是通用的，本章的动作模型能很好地起到抛砖引玉的作用。